Anwendungen der Knotentheorie

Schuhe binden

Überkreuz- und Sägezahnschnürung

Was ist der effizienteste Weg, seine Schuhe zu binden? Ist es die klassische Überkreuzschnürung?

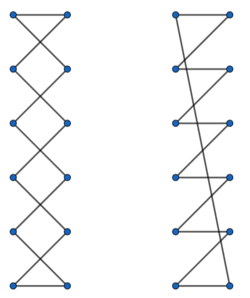
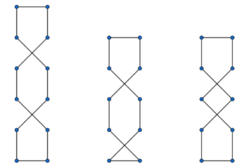
Wir gehen von einem idealen Schuh aus, welcher [math] 2n [/math] Ösen besitzt, [math]n\in \mathbb{N}[/math] auf jeder Seite, um die Schnürsenkel zu binden. Um den Schnürsenkel mathematisch beschreiben zu können, muss er geschlossen sein. In der realen Welt ließe sich dies durch das Binden einer Schleife realisieren. Unsere Schnürung besteht aus [math]2n[/math] Segmenten, wobei ein Segment jeweils die Verbindung zwischen zwei Ösen ist. Das heißt demzufolge auch, dass jede Öse nur einmal verwendet wird. Als weitere Anforderung verlangen wir, dass mindestens eines der beiden einlaufenden Schnürsenkelsegmente je Öse seinen Ursprung in der anderen Reihe der Ösen besitzt. Damit wollen wir sicherstellen, dass die zwei Seiten des Schuhs wirklich festgezogen werden.

Besitzt der Schuh auf jeder Seite gerade [math] n=1[/math] Löcher, so gibt es genau eine Möglichkeit, seinen Schuh zu binden. Betrachten wir also nun einen Schuh mit [math] n\geq2[/math] Löchern auf jeder Seite. Die Anzahl der möglichen Schnürungen bei [math] n[/math] Löchern ergibt sich zu

[math]\#(n)= \frac{(n!)^2}{2} \sum\limits_{k=0}^{m}\frac{1}{n-k}\binom{n-k}{k}^2 [/math]

mit [math] m=n/2[/math] für gerade [math]n[/math] und [math]m=(n-1)/2[/math] für ungerade [math]n[/math].

Unter unseren Voraussetzungen kürzeste Schnürung, links für [math] n[/math] gerade, rechts zwei Beispiele für [math] n[/math] ungerade

Die Länge einer Schnürung ist die Summe aus allen einzelnen Teilsegmenten. Unter der Verwendung von Symmetrien und Vereinfachungen ergibt sich folgendes Muster für die kürzeste Schnürung unter unseren Vorraussetzungen, wobei hier allerdings noch zwischen [math]n[/math] gerade oder ungerade unterschieden werden muss.

Diese Schnürung ist allerdings nicht die stärkste. Der Schnürsenkel funktioniert wie ein Flaschenzug, wenn er die zwei Reihen zusammenzieht. Allerdings hängt die Stärke der Schnürung vom Verhältnis der Abstände zwischen den einzelnen Ösen und den beiden Reihen ab. Es lässt sich ein kritisches Verhältnis [math]x_n[/math] finden, sodass für [math]x\leq x_n[/math]die Überkreuzbindung die stärkste Verbindung ist und für [math] x\geq x_n [/math]die Sägezahnbindung die stärkste Verbindung ist. Für reale Schuhe hingegen ist dieses Verhältnis meistens in der Nähe von [math] x_n[/math], sodass die Art der Bindung keine entscheidende Rolle spielt.

Zwei Nägel und ein Bild

Meist werden Bilder ganz simpel und ohne mathematische Rafinesse an der Wand befestigt wie in Abb. ? gezeigt. Möchte der geschickte Mathematiker jedoch eine Weise finden, das Bild nur durch die Entfernung eines Nagels abhängen zu können (etwa um möglichst energiesparend an den dahinterliegenden Tresor zu gelangen), so braucht es hierfür eine geschicktere Konstruktion.

Eine mächtige Methode, einen geeigneten Knoten zu finden, funktioniert über die freie Gruppe. Definiert man die Erzeuger [math]x_1,{x_1}^{-1},...,x_n, {x_n}^{-1}[/math] während hierbei jeweils [math]x_i[/math] die Umschingung des Nagels [math]i[/math] im Urzeigersinn und [math]{x_i}^{-1}[/math] jene gegen den Uhrzeigersinn beschreibt. Wendet man diese Notation auf das oben beschriebene Problem mit zwei Nägeln an, so kann man sich leicht davon überzeugen, dass [math]x_1x_2{x_1}^{-1}{x_2}^{-1}[/math] eine Lösung ist, die die Voraussetzungen erfüllt. Denn sobald man nun einen Nagel hinauszieht, wir der entsprechende Erzeuger obsolet und es bleibt eine Umschlingung um den anderen Nagel im und eine gegen den Uhrzeigersinn übrig, wodurch das Bild auch diese scheinbare Aufhängung verliert und hinabfällt. Hierfür lohnt es sich bereits, dies als Kommutator [math][x1,x2][/math] einzuführen.

Nun lässt sich diese Erkenntnis auch auf das Problem erweitern, ein Bild mit n Nägeln aufhängen zu wollen, welches erneut durch das Ziehen eines beliebigen Nagels abgehängt werden kann. Für das 3-Nägel-Problem wäre etwa eine Lösung, die bekannte 2-Nägel-Lösung [math]S_2:=x_1x_2{x_1}^{-1}{x_2}^{-1}[/math] zu nutzen und durch [math][S_2,x3]=S_2x_3{S_2}^{-1}{x_3}^{-1}=x_1x_2{x_1}^{-1}{x_2}^{-1}x_3x_2x_1{x_2}^{-1}{x_1}^{-1}{x_3}^{-1}[/math] zu variieren.

Analog ergibt sich für 4 Nägel erneut induktiv die folgende Lösung: [math][S_3,x4]=S_3x_4{S_3}^{-1}{x_4}^{-1}=...=x_1x_2{x_1}^{-1}{x_2}^{-1}x_3x_2x_1{x_2}^{-1}{x_1}^{-1}{x_3}^{-1}x_4x_3x_1x_2{x_1}^{-1}{x_2}^{-1}{x_3}^{-1}x_2x_1{x_2}^{-1}{x_1}^{-1}[/math]

Einziger Nachteil dieser Methode: Man braucht [math]2^n+2^{n-1}-2[/math] Umschlingungen. Beweis folgt.

Stricken

Trivia

Wenn Ihnen dieser Artikel gefallen hat, könnte Ihnen auch das Museumswächterproblem gefallen. ^^