Hyperbolische Geometrie und Physik - Der Minkowski-Raum
Der Minkowski-Raum
Der Minkowski-Raum ist eines der wichtigsten Mittel zur Darstellung der Relativitätstheorie und deren Beschreibung von Raum und Zeit, da diese die Beschränkungen des Euklidischen Raums überschreitet.
In der Differentialgeometrie werden Minkowski-Räume als Vektorräume beliebiger Dimension mit einer symmetrischen Bilinearform der Signatur (1,n) betrachtet,
wohingegen in der Physik hauptsächlich der vierdimensionale Fall behandelt wird. Dieser besitzt die drei Koordinaten des Euklidischen Raums und fügt eine vierte für die Zeit ein, wodurch er zu einer vierdimensionalen Mannigfaltigkeit wird. [1][2]
Der Einfachheit halber wird hier hauptsächlich das hyperbolische Modell mit vier Dimensionen als Pseudo-Euklidischer Raum (endlich-dimensional mit nicht-ausgearteter quadratischer Form) angeführt. Dieser ist anschaulich gut zu verstehen und nimmt die intuitive Vorstellung der Geometrie auf, was den Zugang erleichtert.
Mathematische Struktur
Ausgehend von einem kanonischen Ursprung ist der Minkowski-Raum eine Modellierung der Raumzeit mit einem Vektorraum. Der Erweiterung des Euklidischen Raumes zu einem Pseudo-Euklidischen Raum bedurfte es aufgrund des sonst fehlenden Zusammenhangs von Ort und Zeit, des realen sowie relativen Verlaufes von Objekten. Die Betrachtung dieser Form ist nicht rein physikalisch motiviert, die allgemeine Beschreibung verkompliziert aber das Thema.
Definition
Minkowski-Skalarprodukt des [math] \mathbb{R^{n+1}}[/math]
[math]⟨⟨ x,y ⟩⟩ := -x^0y^0+\sum_{i=1}^nx^iy^i[/math] [3]
In reeller Definition für einen reellen Vektorraum und dessen sog. Minkowski-Vierervektoren(Ereignissen) x und y:
[math]x \in R^3 (R^4) [/math]
[math]x \cdot y := -x_0y_0+x_1y_1+x_2y_2+x_3y_3[/math]
Die Konvention der Signatur der Metrik von (-,+,+,+) ist nicht festgeschrieben, in anderen Anwendungsbereichen als der Relativitätstheorie wird ebenfalls (+,-,-,-) verwendet.
Ebenfalls ist es möglich das innere Produkt zweier Elemente als Wirkung des metrischen Tensors [math]\eta_{\mu,\nu}[/math] aufzufassen, welches als Tensor einer Pseudo-euklidische Metrik der Lorentz'schen Mannigfaltigkeit agiert.[4]
[math]⟨⟨ x,y ⟩⟩ = x * gy,\ \ \ g = diag(-1,.., -1, +1)[/math]
- [math]\eta = \begin{pmatrix}-1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&1\end{pmatrix},[/math]
[math]u \cdot v = \eta(u, v),[/math]
Geometrie und Hyperboloid Modell
Die Bedeutung der Geometrie im Minkowski-Raum ist sehr von der Betrachtung abhängig,er weist nicht die bekannte Euklidische Geometrie, als auch die allgemeine Riemannsche Geometrie, mit intrinsischer Krümmung auf.
Dass heißt das Modell der hyperbolischen Geometrie (negative Krümmung) sowie die durch die Kugel modellierten positiven Krümmung existieren hier im allgemeinen eigentlich nicht, welches durch die Indefinitheit der Minkowski-Metrik begründet ist.
Der Minkowski-Raum ist insbesondere kein metrischer Raum und keine Riemannsche Mannigfaltigkeit mit Riemannscher Metrik. Allerdings Minkowski-Raum enthält Untermannigfaltigkeiten, die mit einer Riemannschen Metrik und mit die hyperbolische Geometrie ausgestattet sind,.
In diesem Kapitel stellen wir das Hyperboloidmodell für den hyperbolischen Raum vor, das als Hyperfläche im Minkowski-Raum definiert ist.
insbesondere und um die Visualisierung zu erleichtern, nehmen wir an dass der Minkowski-Raum [math]M^3[/math]immer dreidimensional ist ( alles ist analog für [math]M^n \; n\in \mathbb{N}[/math]).
Das Hyperboloid, eine Pseudosphäre im Minkowski-Raum, ist der Kugel in der euklidischen Geometrie sehr ähnlich.
Für viele Zwecke ist das Hyperboloid das beste Modell des hyperbolischen Raums: Wir werden insbesondere sehen, dass es ziemlich einfach und elegant ist, alle relevanten geometrischen Eigenschaften zu sehen: die Riemannsche Metrik, Geodäten, Abstandsfunktion und Krümmung.
Konstruktion
Wie bereits erwähnt, verwenden wir den dreidimensionalen Minkowski-Raum, bezeichnet mit [math]M^3[/math] oder [math]R^{1,2}[/math], dessen Metrik gegeben ist durch
[math]d(x,y)=\left \| x-y \right \|= [/math]
gegeben.
Der Ansatz zum Aufbau von unsere Modell von Hiperbolische Raum [math]H^2[/math] und zur Diskussion dieses Modells beginnt mit einer quadratischen Minkowski-Form,
[math]q((x,y,z))=-x^2+y^2+z^2=[x,y,x]\begin{vmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix}[x,y,x]^t=X^tJX.[/math]
mit diese quadratische Form ,wird eine bilineare form ,[math]p[/math], sehr nutzlich in unsere entwicklung des modelles:
[math]für\; alle\; X,Y \in M^3\; [/math]definieren wir eine bilinear form p mit
[math]p(X,Y):=1/2[q(X+Y)-q(X)-q(Y)]=X^tJY[/math].
Sehen wir dass [math] q(X)=p(X,X), [/math] und dass
[math]p(U_i,U_j)=e_i\; für\; i=j [/math]
[math]und\; p(U_i,U_j)=0\; für\; i \ne j\; und\; U_1,...,U_n\; basis\; von\; M^3[/math].
Endlich erhalten wir ein Hyperboloid über den wir Hyperbolische Geometrie modellieren können mit die folgende niveaumenge:
[math] H={(x,y,z)\;in\;M^3\; s.d. \;q(x,y,z)=-1, \; und\; x\gt 0}[/math]
H ist invariant bei Drehungen um die 𝑧-Achse und bei Reflexionen an vertikale Ebenen durch den Ursprung.
Eigenschaften
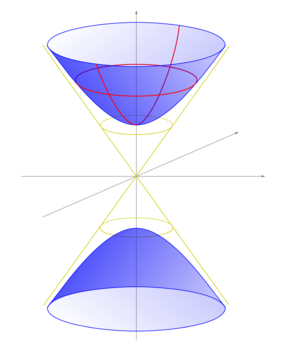
H besitz zwei Zusammenhangs komponenten H+ und H− , die als oberes und unteres Blatt bezeichnet werden.
Andererseits ist ihr Schnittpunkt mit einer vertikalen Ebene eine Hyperbel .
Der obere Bogen dieser Hyperbel mit den hyperbolischen trigonometrischen Funktionen parametrisiert werden kann:
[math] x(u,v)=sinh(u) cos(v) \; y(u,v)=sinh(u) cos(v) \; z(u,v)=cosh(u)[/math]
(dies ist die Erklärung für den Namen Hyperbolische trig-Funktionen).
Das hyperboloide Modell der hyperbolischen Ebene ist die obere Bogen der Hyperbel H+, die mit der Riemannschen Metrik ausgestattet ist, die aus dem Minkowski-Skalarprodukt des gesamten Raums induziert wird.
Das Hyperboloid [math] H^2[/math] selbst ist asymptotisch zum Kegel [math]𝑥^2 + 𝑦^2 − 𝑧^2 = 0 [/math] (erhältlich durch Drehung der Hyperbelachsen), also zum Lichtkegel.
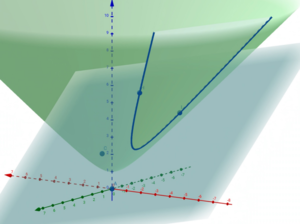
Geraden in [math] H^2[/math] sollen der Schnittpunkt von Ebenen sein, die durch den Ursprung mit der oberen Hälfte der beiden schichtförmigen Hyperboloide q(X) = −1 gehen.
Da drei Punkte eine eindeutige Ebene bestimmen, es folgt, dass durch zwei Punkte von H2 eine eindeutige Gerade existiert.
Zwei unterschiedliche Punkte 𝑝 und 𝑞 in H+ werden durch ein einzigartiges geodätisches Segment verbunden 𝛾 außerdem ist 𝛾 eindeutig und längenminimierend.
Ein wichtiger Satz, der sich aus dieser Beobachtung ergibt, lautet: Der Abstand zwischen zwei beliebigen Punkten 𝑝 und 𝑞 in H+ ist gegeben durch
[math]d(p,q)=arcosh(\mathbf{p}\cdot\mathbf{q} )[/math]
endlich ein weiteres relevantes Merkmal dieses Objekts ist, dass obwohl in [math] R^3[/math]eine seite von eine Hyperboloid hat positive Gaußsche Krümmung der Tatsache, dass es innerhalb des Minkowski-Raums liegt schickt eine negative Gaußsche Krümmung von -1 .
Rolle in der Physik
In den Anwendungen der Physik nimmt die Zeit die neue 0. Koordinate ein während die restlichen Koordinaten (normalerweise 3) die räumlichen sind ( [math] v=(t,x_1,x_2,x_3)[/math]. In relativistischer Physik sind Längen, Geschwindigkeiten (bis auf die Lichtgeschwindigkeit) und sogar die Gleichzeitigkeit von Ereignissen (so nennen wir Punkte bzw. Vektoren im Minkowskiraum) vom Betrachter abhängig, den wir deshalb immer in den (räumlichen) Ursprung unseres Koordinatensystems setzen, da er natürlich zu sich selbst keinen Abstand beobachtet. Da dies immer so bleibt bewegt er sich entlang der Zeitachse.
Ein wichtiges physikalisches Werkzeug auf Minkowskiräumen ist der Lichtkegel. Um die Darstellung zu vereinfachen wird oft nur eine Raumkoordinate betrachtet, wobei die Zeitachse nach oben und die Raumachse nach rechts zeigt und die Skalierung der Achsen so gewählt wird, dass der Pfad eines Objekts, das sich vom Ursprung aus mit Lichtgeschwindigkeit bewegt, auf unserer Darstellung, dem sogenannten Minkowski-Diagramm, entlang einer 45°-Gerade bewegt. Diese Geraden (da die Bewegung sowohl in positive als auch negative x-Richtung geschehen kann) bilden einen Doppelkegel, den sogenannten Lichtkegel. Diesen Lichtkegel gibt es natürlich auch für höhere Dimensionen.
Der Licht-Doppelkegel teilt den Minkowskiraum in drei Teile: Die Vektoren/Ereignisse im Inneren des Doppelkegels nennen wir zeitartig, für sie ist [math] \langle v,v\rangle\lt 0 [/math], die Vektoren/Ereignisse am Rand (die Intuitive, nicht die mathematische Version) des Lichtkegels nennen wir lichtartig, für sie ist [math] \langle v,v\rangle=0 [/math]. Diese beiden bilden zusammen die sogenannten kausalen Vektoren/Ereignisse, sie können Einfluss auf das Ereignis im Ursprung haben oder von ihm beeinflusst werden. Das hängt davon ab ob sie zur kausalen Vergangenheit oder Zukunft gehören, also ihr t-Wert kleiner oder größer 0 ist. Die restlichen Vektoren/Ereignisse, die sich also außerhalb des Licht-Doppelkegels befinden nennen wir Raumartig, für sie ist [math] \langle v,v\rangle\gt 0 [/math] sie sind nicht kausal (manchmal ist auch der Ursprung als Raumartig definiert).
[Führe hier Lorentz Transformation über einen neuen Beobachter von Urpsrungsereignis aus mit nicht0 geschwindigkeit bzgl originalbeobachter ein. Lorentz transformation soll zeitkegel erhalten und "artigkeit" von vektoren bleibt unter lorentz trf erhalten (führe vllt die formeln für geschw. zeit usw. ein statt nur allg. zu bleiben). Weiterhin kann man eine Matrix die eine lorentz trf beschreibt durch eine (-1 & 0\\ 0 & A) erhalten, wobei A in O(n-1) ist. vorzeichen bin ich mir nicht sicher. Poincare bin ich mir nicht sicher, weil das eine Lorentz trf mit einer verschiebung kombiniert ist. Vllt später noch zwillingsparadoxon, dazu dann sagen dass beschl. miteinbezogen werden muss und das erst in ART passiert (out of scope?). Vllt noch Energie-Impuls-viervektor]
Kausalstruktur, Gleichzeitigkeit, (Paradoxien?) Transformationseigenschaften, Boosts (Poincare-Gruppe) Invarianten
Erhellende Bilder?
Zusammenhang mit Poincare Disk/Ball-Modell?
Einzelnachweise und Quellen
letzter Zugriff für alle: 19.09.2021
Autoren
Lela Eigenrauch, Henry Bertels, Elia Fiammengo, Falk Loewner