Hyperbolische Geometrie und Physik - Der Minkowski-Raum
Der Minkowski-Raum
Der Minkowski-Raum ist eines der wichtigsten Mittel zur Darstellung der Relativitätstheorie und deren Beschreibung von Raum und Zeit, da diese die Beschränkungen des Euklidischen Raums überschreitet.
In der Differentialgeometrie werden Minkowski-Räume als Vektorräume der Dimension n+1 mit einer symmetrischen Bilinearform der Signatur (n,1) betrachtet, wohingegen in der Physik hauptsächlich der vierdimensionale Fall behandelt wird. Dieser besitzt die drei Koordinaten des Euklidischen Raums und fügt eine vierte für die Zeit ein, wodurch er zu einer vierdimensionalen Mannigfaltigkeit wird. [1][2]
Der Minkowski-Raum modelliert die Raumzeit mit einem 4-dimensionalen Vektorraum, auf dem eine Bilinearform definiert wird und der eine konsistente Beschreibung von Relativbewegungen bei invarianter Lichtgeschwindigkeit erlaubt.
Der Einfachheit halber wird hier hauptsächlich das hyperbolische Modell mit vier Dimensionen als Pseudo-Euklidischer Raum (endlich-dimensional mit nicht-ausgearteter quadratischer Form) angeführt. Dieser ist anschaulich gut zu verstehen und nimmt die intuitive Vorstellung der Geometrie auf, was den Zugang erleichtert.
Mathematische Struktur
Definition
Die Minkowski-Raumzeit ist ein 4-dimensionaler reeller Vektorraum [math]\mathcal{M}[/math] mit einer indefiniten, nicht-ausgearteten, symmetrischen Bilinearform [math]g[/math] mit Signatur (3,1).[3][4]
Auf [math]\mathcal{M}[/math] ist das Lorentzsche innere Produkt [math]g(x,y) := -x^0y^0+\sum_{i=1}^nx^iy^i[/math]. [5] In der 4-dimensionalen Minkowski-Raumzeit ist also [math]g(x,y) = - x^0 y^0 + x^1 y^1 + x^2 y^2 + x^3 y^3[/math] und wird dort Minkowski Bilinearform genannt.
Ebenfalls ist es möglich, die Bilinearform als Wirkung des metrischen Tensors
- [math]\eta_{\mu,\nu} = \begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}[/math]
auf einer Mannigfaltigkeit aufzufassen, wobei [math]\eta[/math] als Tensor einer Pseudo-euklidischen Metrik der Lorentz'schen Mannigfaltigkeit agiert:[2]
- [math]g(x,y)\;\hat{=}\;\eta^{\mu\nu}x_\mu y_\nu[/math].
Da das Lorentzsche innere Produkt nicht positiv definit ist, gibt es nicht-triviale Vektoren [math]v[/math] in [math]\mathcal{M}[/math], die [math]g(v,v) = 0[/math] erfüllen. Diese heißen lichtartig und [math]\mathcal{M}[/math] besitzt eine Basis aus solchen lichtartigen Vektoren, welche jedoch nie orthogonal ist.
Die Konvention der Signatur [math](-,+,+,+)[/math] der Metrik ist nicht festgeschrieben, in anderen Anwendungsbereichen als der Relativitätstheorie wird ebenfalls [math](+,-,-,-)[/math] verwendet.
Geometrie und Hyperboloid-Modell
Der Minkowski-Raum kann nicht mit der euklidischen und generalisierten riemannschen Geometrie ausgestatten werden, da die Minkowski-Metrik indefinit ist.
Insbesondere ist der Minkowski-Raum selbst kein metrischer Raum und keine Riemannsche Mannigfaltigkeit. Allerdings enthält er Untermannigfaltigkeiten, die mit einer riemannschen Metrik und hyperbolischen Geometrie ausgestattet werden können.[1]
Hier soll das speziellere Hyperboloidmodell für den hyperbolischen Raum erläutert werden, das als Hyperfläche im Minkowski-Raum definiert ist.
Für eine einfachere Visualisierung wird vorausgesetzt, dass der Minkowski-Raum [math]\mathcal{M^3}[/math] dreidimensional definiert ist (analog für [math]\mathcal{M^n}, \; n\in \mathbb{N}[/math]).
Für viele Anwendungen ist diese Modell des hyperbolischen Raums das geeignetste, da es alle relevanten geometrischen Eigenschaften aufzeigt: die riemannsche Metrik der Untermannigfaltigkeiten, Geodäten, die Abstandsfunktion und die Krümmung.
Konstruktion
Der Ansatz zum Aufbau der hyperbolischen Ebene [math]H^2[/math] und zur Diskussion dieses Modells beginnt mit der Wahl einer quadratischen Form:
[math]g((x,y,z))=-x^2+y^2+z^2=[x,y,z]\begin{vmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix}[x,y,z]^t=X^tJX[/math].
Mithilfe dieser Funktion können wir einen Hyperboloid als folgende Niveaumenge definieren :
[math]H=\left \{ {(x,y,z)\;\in\;\mathcal{M^3}\;q(x,y,z)=-1\;\wedge\; x\gt 0} \right \}[/math].
Außerdem ist [math]H[/math] mit der hyperbolischen Geometrie versehen und invariant bei Drehungen um die 𝑧-Achse wie auch bei Reflexionen an der vertikalen Ebene durch den Ursprung.
Analytische Eigenschaften
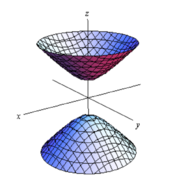
[math]H[/math] besitzt zwei Zusammenhangskomponenten, [math]H+[/math] und [math]H-[/math], die als oberes und unteres Blatt bezeichnet werden. Die Schnittpunkte der beiden mit einer vertikalen Ebene bilden eine Hyperbel.
Der obere Bogen dieses Hyperboloids kann mit den hyperbolisch-trigonometrischen Funktionen parametrisiert werden, wie es oft in der Physik geschieht:
[math]x(u,v)=sinh(u) cos(v), \; y(u,v)=sinh(u) cos(v), \; z(u,v)=cosh(u)[/math]
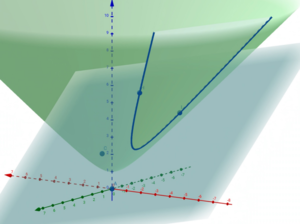
Das Hyperboloid-Modell besteht aus dem oberen Bogen der Hyperbel [math]H+[/math] mit der Riemannschen Metrik, die von der Minkowski-Bilinearform induziert wird.
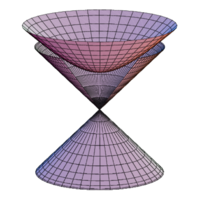
Dieses Hyperboloid, [math]H^2[/math], selbst ist asymptotisch zum (Licht-)kegel [math]𝑥^2 + 𝑦^2 − 𝑧^2 = 0[/math] (durch Drehung der Hyperbelachsen).
Eine Gerade zwischen zwei Punkten [math]𝑝[/math] und [math]𝑞[/math] in [math]H^2[/math] ist definiert als Schnittmenge zwischen der Ebene, die durch den Ursprung sowie [math]𝑝[/math] und [math]𝑞[/math] läuft, und des Hyperboloids selbst. Diese Geraden, die auf dem Hyperboloid liegen, können auf eine Scheibe in der x-y-Ebene projeziert werden und damit erhält man das Poincaré-Scheiben-Modell der Hyperbolischen Geometrie.
Der Abstand zwischen zwei beliebigen Punkten [math]𝑝[/math] und [math]𝑞[/math] in [math]H^2[/math] ist auch mit hyperbolisch-trigonometrischen Funktionen gegeben:
[math]d(p,q)=arcosh(\mathbf{p}\cdot\mathbf{q} )[/math][6]
Ein weiteres relevantes Merkmal dieses Modells ist, dass obwohl in [math]R^3[/math] das Hyperboloid positive Gaußsche Krümmung hat, die Tatsache, dass es innerhalb des Minkowski-Raums liegt, der eine negative Gaußsche Krümmung von -1 besitzt.[6]
Anwendung in der Physik
Die Punkte in [math]\mathcal{M}[/math] werden Ereignisse genannt und man kann ihnen nach Wahl eines Inertialsystems einen relativen Zeitpunkt und Ort zuweisen (ein Inertialsystem ist ein unbeschleunigtes Bezugssystem).
Hierbei nimmt die Zeit die 0. Koordinate ein während die restlichen Koordinaten (normalerweise 3) die räumlichen sind, sodass [math] x=(t,x_1,x_2,x_3)[/math].
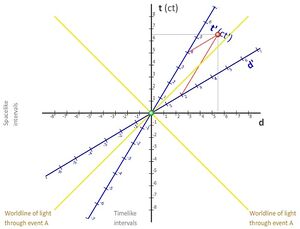
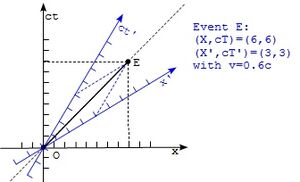
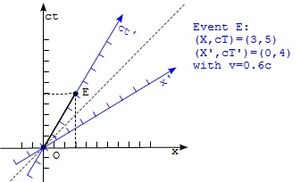
In relativistischer Physik werden Längen, vergehende Zeit und Geschwindigkeiten von Beobachtern, die sich relativ zueinander unterschiedlich schnell bewegen, unterschiedlich wahrgenommen. Graphisch stellt man dies in einem Minkowski-Diagramm dar, welches zur Vereinfachung nur eine Zeit und eine x-Achse hat.
Die Skalierung ist so gewählt, dass Lichtgeschwindigkeit einer Steigung von 1 entspricht. Der Beobachter dieses Systems ist hierbei immer bei [math] x=0 [/math] . Ein zweiter Beobachter, der den Ursprung durchquert und sich mit einer Geschwindigkeit [math] v [/math] relativ zum ersten Beobachter bewegt wird durch neue Achsen [math] x' [/math] und [math] ct' [/math] dargestellt.
Für den Winkel zwischen den Achsen der beiden Beobachter gilt: [math] \tan(\alpha)=\frac{v}{c} [/math]
Das Maß der Achsen des bewegten Beobachters wird um [math] \frac{\sqrt{1+\left(\frac{v}{c}\right)^2}}{\sqrt{1-\left(\frac{v}{c}\right)^2}} [/math] skaliert.
Ereignisse auf einer Geraden parallel zur x'-Achse nimmt der bewegte Beobachter als gleichzeitig wahr, Ereignisse auf einer Geraden parallel zur ct'-Achse als gleichweit entfernt.[7]
Dadurch interpretieren sie z.B. den Zeitpunkt desselben Ereignisses unterschiedlich voneinander. Ereignisse auf dem Lichtkegel des Ursprungsereignisses und die Lichtgeschwindigkeit nimmt jedoch jeder Beobachter gleich wahr.[8]
Eine Lorentz-Transformation erlaubt es rechnerisch vom Inertialsystem (ein gleichmäßig bewegtes Bezugssystem) des ersten zu dem des zweiten Beobachters überzugehen. Dazu definiert man [math] \beta = \frac{v}{c} [/math] und den Lorentz-Faktor [math] \gamma=\frac{1}{\sqrt{1-\beta^2}} [/math]
Dann ist [math] x'=\gamma(x-\beta\cdot ct) [/math]und [math] ct'=\gamma(ct-\beta \cdot x) [/math][9].
Die Darstellungsmatrizen allgemeiner Lorentztransformationen höherer Raumdimensionen haben z.B. die Form [math] A=\begin{pmatrix} 1&0\\ 0&B\\ \end{pmatrix} [/math], wobei [math] B\in O(n) [/math] eine orthogonale Matrix ist.
Übergänge zwischen Inertialsystemen, die bei t=0 übereinstimmen, sogenannte Lorentz-Boosts, haben die Form
[math] A=\begin{pmatrix} \cosh(\phi)&\sinh(\phi)&0\\ \sinh(\phi)&\cosh(\phi)&0\\ 0&0&E_{n-1} \end{pmatrix} [/math] [10],
wobei [math] \phi\in\mathbb{R} [/math] und [math] E [/math] die Einheitsmatrix ist. Unter allgemeinen Lorentz-Transformationen bleibt die Minkowski-Bilinearform invariant.
Der Licht-Doppelkegel teilt den Minkowskiraum in drei Teile: Die Vektoren/Ereignisse im Inneren des Doppelkegels heißen zeitartig, für sie ist [math] g(x,x)\lt 0 [/math], die Vektoren/Ereignisse am Rand des Lichtkegels heißen lichtartig, für sie ist [math] g(x,x)=0 [/math].
Diese beiden bilden zusammen die sogenannten kausalen Vektoren/Ereignisse, sie können Einfluss auf das Ereignis im Ursprung haben oder von ihm beeinflusst werden.
Das hängt davon ab ob sie zur kausalen Vergangenheit ([math] t\lt 0 [/math]) oder Zukunft ([math] t\gt 0 [/math]) gehören.
Die Vektoren/Ereignisse, die sich außerhalb des Licht-Doppelkegels befinden heißen Raumartig, für sie ist [math] g(x,x)\gt 0 [/math]. Sie sind nicht kausal (manchmal ist auch der Ursprung als Raumartig definiert).
Da die Minkowski-Bilinearform invariant ist, ist auch die Kausalität unter Lorentz-Transformationen erhalten.
Einzelnachweise und Quellen
- ↑ 1,0 1,1 https://en.wikipedia.org/wiki/Minkowski_space
- ↑ 2,0 2,1 https://de.wikipedia.org/wiki/Minkowski-Raum
- ↑ Gregory L. Naber, "The Geometry of Minkowski Spacetime", Applied Mathematical Sciences 92, Springer-Verlag New York, 2012, ISBN: 978-1-4419-7837-0,978-1-4419-7838-7
- ↑ https://de.wikipedia.org/wiki/Signatur_(Lineare_Algebra)
- ↑ https://www.math.uni-potsdam.de/fileadmin/user_upload/Prof-Geometrie/Dokumente/Lehre/Veranstaltungen/WS0405-SS08/LorentzianGeometryEnglish13Jan2020.pdf
- ↑ 6,0 6,1 https://arxiv.org/pdf/2003.11180.pdf
- ↑ https://www.herongyang.com/Physics/Minkowski-What-Is-Minkowski-Diagram.html
- ↑ https://www.herongyang.com/Physics/Minkowski-Diagram-Constancy-of-Speed-of-Light.html
- ↑ https://www.herongyang.com/Physics/Minkowski-What-Is-Lorentz-Transformation.html
- ↑ https://www.math.uni-potsdam.de/fileadmin/user_upload/Prof-Geometrie/Dokumente/Lehre/Veranstaltungen/WS0405-SS08/LorentzianGeometryEnglish13Jan2020.pdf Example 1.15
letzter Zugriff für alle: 19.09.2021
Autoren
Lela Eigenrauch, Henry Bertels, Elia Fiammengo, Falk Loewner