Zufallsmatrizen - Bohemians und die geheimnisvolle Ordnung im Chaos

Hier entsteht eine tolle Seite ... bis dahin noch etwas Geduld! :D

Zufallsmatrizen

Definition

Eine Zufallsmatrix ist eine Matrix, deren Einträge teils oder ganz zufällig sind.

[math] \frac{N_{f,H} - \int f(\lambda) \, dN(\lambda)}{\sigma_{f, n}} \overset{D}{\longrightarrow} N(0, 1) [/math]

Bohemian Matrices

Inhalt

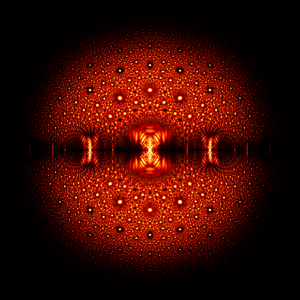
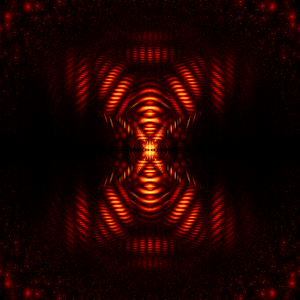
Galerie

Betaverteilung

Eigenwertdichte von 15 Millionen [math]6\times 6[/math] Matrizen mit Werten aus einer Betaverteilung mit den Parametern [math] \alpha = 0,001, \beta = 0,001 [/math] (Die Eigenwerte wurden an der imaginären Achse gespiegelt)

Noch ´ne Betaverteilung

Zufällige Matrix mit Einträgen aus diskreter Menge

Eigenwertdichte von 10 Millionen [math]6 \times 6[/math] Matrizen mit Einträgen aus der Menge [math] \{-1, -\frac{1}{1000}, 0, \frac{1}{1000}, 1\} [/math]

Zoom in die Mitte des obigen Bildes

Obere Hessenbergmatrix

Eigenwertdichte von 20 Millionen [math]12 \times 12[/math] oberer Hessenbergmatrizen mit Toeplitz-Struktur und Einträgen aus der Menge [math]\{-1, 0, 1\}[/math]

Tridiagonalmatrix

Eigenwertdichte von 10 Millionen [math]10 \times 10[/math] Tridiagonalmatrizen mit Einträgen aus der Menge [math]\{-π, π\}[/math]

Feste Matrix mit kontinuierlicher Verteilung in bestimmten Werten (Eigenfish)

Hier wurden Matrizen von der Form [math]\begin{pmatrix} 0 & 0 & 0 & A \\ -1 & -1 & 0 & 0 \\ B & 0 & 0 & 0 \\ -1 & 1 & 1 & -1 \end{pmatrix}[/math]

Eigenwertdichte einer Menge von Matrizen

Irgendwas mit π

Trivia (vor oder nach Galerie?)

Zufallsmatrizen können in den unterschiedlichsten, teils überraschenden Themengebieten genutzt werden, um (Natur-)Phänomene zu beschreiben oder Daten zu modellieren. So etwa bei:

• Abständen parkender Autos und von Bäumen im Urwald
• Verknüpfung von Neuronen im Gehirn
• Datenkompression, Mobilfunk
• Finanzwirtschaft (Fluktuation von Börsenkursen)
• der Statistik ankommender U-Bahnen in New York

Warum genau es so gut funktioniert, diese doch sehr unterschiedlichen Dinge treffend durch Zufallsmatrizen zu beschreiben, ist überwiegend unbekannt.

Nicht nur in praktischen Anwendungsgebieten werden Zufallsmatrizen benutzt: Auch bei theoretischeren Problemen in der Mathematik, wie dem Beweis der Riemannschen Vermutung, sind Zufallsmatrizen möglicherweise ein vielversprechender Ansatz, zu einer Lösung zu gelangen, bspw. über eine Matrix, von den Wissenschaftlern Riemannium getauft, deren Eigenwerte den Nullstellen der Riemannschen Zeta-Funktion entsprechen.

Quellen und Links

Quellen