Fibonacci Folge

Die Fibonacci-Folge ist eine Folge reeller Zahlen.

Erweiterung auf ganze Zahlen

Die Bildungsvorschrift lässt sich einfach umstellen:

[math] f_{n}=f_{n+2}-f_{n+1} [/math]

Damit erhält man eine erweiterte Fibonacci-Folge:

[math] \cdots\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} f_{-7} & f_{-6} & f_{-5} & f_{-4} & f_{-3} & f_{-2} & f_{-1} & f_0 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7\\\hline 13 & -8 & 5 & -3 & 2 & -1 & 1 & 0 & 1 & 1 & 2 & 3 & 5 & 8 & 13 \end{array} \cdots [/math]

Die Beträge der Werte sind symmetrisch, im Negtiaven alternieren sie jedoch. Dementsprechend nähert sich das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen im Negativen gegen [math]-\frac{1}{\Phi}[/math] an.

Bei der Fibonacci-Folge sind die ersten beiden Glieder 1. Also [math]f_1 = f_2 = 1[/math]. Damit ist die Fibonaccifolge vollständig definiert. Ein anderes Beispiel ist, wenn man statt [math]f_1 = f_2 = 1, f_1 = 1[/math] und [math]f_2 = 2[/math] nimmt bekommt man die Lucas Folge.

Kaninchen-Aufgabe

Eine Anwendungsbeispiel findet die Fibonacci Folge bei der Kaninchenpopulation.

Es startet ein männliches und ein weibliches Kaninchenneugeborenes (ein Paar). Angenommen ein Neugeborenes braucht ein Monat um auszuwachsen, ein Paar bekommt pro Monat ein Paar neugeborenes und kein Kaninchen stirbt.

Im ersten Monat sind es also ein Paar Neugebore, im 2. Monat sind sie Erwachsen, also keine Neugeborenen. Dann bekommen sie ein Paar Neugeborene. [...]

Es gibt also im ersten Monat keine Erwachsenen, im zweiten Monat dann ein Paar Erwachsene, 3. Monat 1 Paar, 4. Monat 2 Paare [...].

Wenn man sich nun also die Gesamtpopulation anguckt folgt:

[math] \begin{align*} \begin{array}[h]{l|c|c|c|c|c|c} Monat & 1 & 2 & 3 & 4 & 5 & 6\\ \hline Erwachsene & 0 & 1 & 1 & 2 & 3 & 5 \\ \hline Neugeborene & 1 & 0 & 1 & 1 & 2 & 3 \\ \hline Gesamt & 1 & 1 & 2 & 3 & 5 & 8\\ \end{array} \end{align*} [/math]

Hier in dem vereinfachten Beispiel beschreibt also die Fibonaccifolge die Gesamtpopulation der Kaninchen.

Matrixdarstellung

Man kann also die Fibonacci Folge auf verschiedene Weisen darstellen. Hier ein Beispiel für die Darstellung in einer Matrix:

[math]\begin{align*} \left( \begin{array}{cc} 1&1 \\ 1&0 \end{array} \right)^n = \left( \begin{array}{cc} f_{n+1}& f_n \\ f_n & f_{n-1} \end{array} \right) \end{align*}[/math]

Die n-te potenz der Matrix [math]A = \left( \begin{array}{cc} 1&1 \\1&0 \end{array} \right)[/math] gibt die n-te Fibonaccizahl auf der Gegendiagonalen an.

Pisano-Folge

Betrachten wir nun den Restklassenkörper modulo einer Primzahl[[math]\mathbb{Z}/p\mathbb{Z}[/math] mit [math]p \in \mathbb{P}[/math]]. Das für uns relevante ist, sind lediglich die Restklassen [math][x] = \{\ x + np \in \mathbb{Z} \ |\ n \in \mathbb{Z}\ \}[/math]

Bsp: Wir haben [math]\mathbb{Z}/3\mathbb{Z}[/math]

Dann ist [math]7 \in [1][/math], da [math]\frac{7}{3} = 2[/math] Rest 1 ist.

Nun gucken wir uns die Fibonaccifolge an:

0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,121393,196418,317811,514229,832040,1346269

sind also alle Element der Natürlichen Zahlen.

Als nächstes betrachten wir die Fibonaccifolge auf [math]\mathbb{Z/7\mathbb{Z}}[/math]

wir bekommen:

0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1,0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1,0

Spannend hier zu sehen, dass die Folge sich nach 16 Werten wiederholt. Außerdem ist die Restklassenfolge wieder eine Fibonaccifolge, da [math]f_n=f_{n-1}+f_{n-2}[/math] man braucht also nicht die Restklasse von jeder einzelnen Werte der Fibonaccifolge in [math]\mathbb{Z}[/math] bilden, sondern kann die Folge direkt in der Restklasse bilden

Auf [math]\mathbb{Z/2\mathbb{Z}}[/math] wiederholt sich die Folge nach 3 Schritten: 0,1,1....

[math]\mathbb{Z/3\mathbb{Z}}[/math] nach 8 Schritten: 0,1,1,2,0,2,2,1,0....

Goldener Schnitt

Es gibt bei der Konstruktion des goldenen Schnitts stehts zwei Möglichkeiten daran zu gehen. Es gibt Varianten, die sich mit dem inneren und welche die sich mit dem äußeren verhältnis beschäftigen. Innere varianten nehmen eine Stecke und teilen die im goldenen Schnitt. Die äußeren Varianten konstuiren zu einer gegebenen Strecke a eine Teilstrecke b, sodass die beiden im goldenen Verhältnis zueinander stehen.

Konstriktion goldener Schnitt mit innerer und äußeren Teilung

Die einfachste Konstruktion des goldenen Schnittes ist über ein Dreieck. Man zeichne zuerst die Grundseite k ([math]\overline{AB}[/math]) und teilt diese in der Hälfte. Wir bekommen nun 2 Strecken mit der Länge k/2. Als nächstes zeichnen wir orthogonal zu B eine Strecke mit der Länge k/2 ([math]\overline{BC}[/math]) und vervollständigen das Dreicek. Als nächstes konstruieren wir einen Kreis (L) um C herum mit dem Radius k/2. Zum Schluss zeichnen wir um A einen Kreis(M), der vom Radius den Schnittpunkt von dem Kreis L mit [math]\overline{AC}[/math] besitzt bzw. [math]r_M= \overline{AC}-k/2[/math]. Der Schnittpunkt des Kreises M und [math]\overline{AB}[/math] teilt die Strecke [math]\overline{AB}[/math] im goldenen Verhältnis.

[math] \begin{align*} \text{wir wissen} \frac{a}{b}= \phi\\ \text{Beweis} : k &=a+b\\ k^2+\left( \frac{k}{2}\right)^2 &= \left( a+ \frac{k}{2} \right)^2\\ \Leftrightarrow k^2+\frac{k^2}{4} &= a^2 + ak+ \frac{k^2}{4}| \text{ersetze k durch a+b} \\ \Leftrightarrow a^2 + 2ab + b^2 &= a^2 + a^2 + ab\\ \Leftrightarrow b^2 + ab &= a^2 \ \text{(Gleichung für den goldenen Schnitt)} \end{align*} [/math]

mit inneren Teilung konstruiert.

Desweiteren können wir auch das Verhältnis des goldenen Schnitts durch äußere Teilung bekommen.

Zunächst zeichnen wir eine Stecke [math]\overline{AB}[/math] mit der Länge a. Am Punkt B zeichnen wir orthogonal eine Strecke [math]\overline{BC}[/math] auch mit der Länge a. Nun wird der Punkt C mit dem Mittelpunkt M von [math]\overline{AB}[/math] verbunden. [math]\overline{CM}[/math] bildet den Radius eines Kreises. [math]\overline{AB}[/math] wird in Richtung des Kreises verlängert zum Punkt D. [math]\overline{BD}[/math] bildet unser b. Auch hier gilt wieder [math]\frac{a}{b}= \Phi[/math]

Beweis: Wir wissen, dass [math]\overline{AB} = \overline{BC}=a[/math] und [math]\overline{AM}=\frac{a}{2}[/math] und k = a + b mit [math]\frac{a}{b}= \Phi[/math]

[math] \begin{align*} \Rightarrow \overline{CM} = \sqrt{\left(\frac{a}{2}\right)^2+a^2} = \sqrt{\frac{5 a^2}{4}} = \sqrt{\frac{5}{4}}a\\ \Rightarrow k = a + b = \frac{a}{2} + \sqrt{\frac{5}{4}}a= a + \sqrt{\frac{5}{4}} a - \frac{a}{2}a \\ \Rightarrow \Phi =\frac{a}{b} \hat{=} \frac{a}{\sqrt{\frac{5}{4}}-\frac{a}{2}} = \frac{1}{\sqrt{\frac{5}{4}}-\frac{1}{2}} =1,61803... = \Phi \end{align*} [/math]

Goldenes Rechteck

Wir beginnen mit einem Rechteck, bestehend aus einem Quadrat mit den Seitenlängen a und einem rechteck mit den Seitenlängen a und b. Und es gilt wieder $\frac{a}{b}=\phi$.

Die Strecke a kann wieder in eine Strecke b und eine Länge a-b (Stetige Teilung), dann wissen wir, dass wir wieder ein goldenes Rechteck haben. Das kann unendlich weitergeführt werden.

Goldenes Dreieck

Wir haben ein gleichschenkliges Dreieck. Die langen Seiten bezeichnen wir mit k und die kürzere Seite mit a. Es gilt wieder [math]\frac{k}{a}=\Phi[/math]. Um eine Ecke der kürzeren Strecke wird nun ein Kreis L mit der Radius A geszeichnet. Der Schnittpunkt an der gegenüberliegenden Seite des Kreismittelpunktes teilt nun die Seite der Länge im goldenen Verhältnis. Es entsteht ein gleichschenkliges Dreieck mit spitzem Winkel und ein zweites mit einem stumpfen Winkel. Das zweite hat die Seitenlängen k und s.\\

Mit [math]\frac{k}{a}=\Phi[/math] können wir auch die Winkel im Dreieck berechnen:

[math] \begin{align*} \cos(\alpha) &= \frac{\frac{a}{2}}{k} = \frac{a}{2k} = \frac{1}{2\Phi}\\ \Leftrightarrow \alpha &= 72°\\ \end{align*} [/math]

Damit bekommen wir:

[math] \begin{align*} 180° - 90° - 72° = 18° \rightarrow \beta &= 36° \\ \text{oder:}\quad \beta = \quad 2 \sin\left(\frac{1}{2\Phi}\right) &= 36° \end{align*} [/math]

Im stumpfwinkligen Dreieck bekommen wir noch einen Winkel: [math]180° - 2 \cdot 36° = 108°[/math]\\

Da der Winkel an der Spitze des spizwinkligen gleichschenkligen Dreiecks 36° beträgt ist es möglich daraus ein 10-Eck zu bilden mit 10 goldenen Dreiecken.

Pentagramm

[Error:404Page not found]

Goldener Winkel

Der goldene Winkel ist in der Natur relevant. Man betrachtet einen Kreis und teilt ihn in 2 Segmente, so dass der eine Teilumfang a und der andere b im goldenen Verhältnis stehen. Dabei ergibt sich ein Winkel indem man den Vollwinkel durch den goldenen Schnitt teilt$\frac{2 \pi}{\Phi} \approx 222,5°$ \\ Und $2\pi - \frac{2 \pi}{\Phi} \approx 137,5 = \Psi $

Um viel Licht abzubekommen, versuchen Pflanzen ihre Blätter so zu legen, dass möglichst wenige übereinander liegen.

Um anzugeben, wie oft ich ein weiteres Blatt um einen gewissen Winkel $\alpha$ verschiebe, bis ein Blatt ein anderes wieder verdeckt, hilft folgende Formel:

\begin{align*}

n \alpha = k 360° \quad \Leftrightarrow \alpha = \frac{k}{n}360°\quad k,n \in \mathbb{N}

\end{align*}

n gibt an, wie viele Blätter ich hinzufügen kann; k gibt ein vielfaches von 360° an.

Optimal für eine Pflanze ist also das kleinste n für das die Formel erfüllt werden kann, groß ist, da so die Pflanze viel Licht bekommt. Wenn $\alpha$ irrational ist, kann es schlecht bis gar nicht als Bruch dargestellt werden. Je irrationaler eine Zahl also ist, dann sie umso schlechter als Bruch angenähert werden. Mit der Bedingung bietet sich die irrationalste Zahl $\Phi $ an bzw als Winkel $\Psi$.

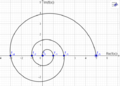
Goldene Spirale

Die goldene Spirale lässt sich graphisch darstellen, indem man rekkursiv goldene Rechtecke zeichnet und dabei in jedem neuen Rehcteck ein neues goldenes Rechteck reinzeichnet. Dabei ist interessant, dass dort die Fibonacci-Folge wieder auftritt. Die einzelnen aufeinanderfolgenden Quadrate haben als Seitenlänge die Werte der Fíbonaccifolge.\\

Man kann die Spirale auch als durch eine konkrete Formel berechnen: $r(\Theta) = ae^{k\theta} = a \Phi^{\frac{2\theta}{\pi}}$

Kontinuierliche Fibonacci-Funktion

Formel von Moivre-Binet

Die Formel von Moivre und Binet ist eine Formel zur expliziten Berechung der n-ten Fibonacci-Zahl:

[math] f_n=\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}[/math]

[math]\Phi[/math] ist dabei der goldener Schnitt [math]\Phi=\frac{1+\sqrt{5}}{2}[/math]. Diese Formel liefert für ganzzahlige Werte für n auch exakte, ganzzahlige Ergebnisse.

Beweis durch vollständige Induktion
. Um zu zeigen, dass diese Formel die Fibonacci-Zahlen ergibt, überprüfen wir die Bildungsvorschrift: IA: Die Formel gilt für [math]n=0\ \left(\frac{\Phi^0-(1-\Phi)^0}{\sqrt{5}}=\frac{1-1}{\sqrt{5}}=0=f_0\right)[/math] und für [math] n=1\ \left( f_1= \frac{\Phi^1-(1-\Phi)^1}{\sqrt{5}}=\frac{\sqrt{5}}{\sqrt{5}}=1=f_1\right)[/math]. IV: Nun gelte sie für ein [math] n,\ n-1\in\mathbb{N}[/math]. IS: Dann gilt: [math] \begin{array}{rl} f_{n+1}=f_{n}+f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n+\Phi^{n-1}-(1-\Phi)^{n-1}}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(1+\Phi)-(1-\Phi)^{n-1}\left(1+(1-\Phi)\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(\Phi^2)-(1-\Phi)^{n-1}(1-\Phi)^2}{\sqrt{5}}\\ &=\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\sqrt{5}} \end{array} [/math] Ebenso für negative Zahlen: [math] \begin{array}{rl} f_{n-2}=f_{n}-f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n-\Phi^{n-1}+(1-\Phi)^{n-1}}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(\Phi-1)-(1-\Phi)^{n-1}\left((1-\Phi)-1\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}\left(\frac{1}{\Phi}\right)-(1-\Phi)^{n-1}\left(\frac{1}{1-\Phi}\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-2}-(1-\Phi)^{n-2}}{\sqrt{5}} \end{array} [/math]

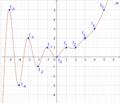
Erweiterung auf eine kontinuierliche Funktion

Nun stellt sich die Frage, was passiert, wenn wir in die Formel von Moivre-Binet nicht-ganzzahlige Werte für n einsetzen, die Fibonacci-Folge also in eine kontinuierliche Funktion umwandeln. Da [math]1-\Phi[/math] jedoch negativ ist, und nicht-ganzzahlige Potenzen von negativen Zahlen nur im Komplexen definiert sind, müssen wir den Wertebereich auf [math]\mathbb{C}[/math] erweitern:

[math] \begin{array}{rl} f:&\mathbb{R}\to\mathbb{C}\\&x\mapsto f(x)=\frac{\Phi^x-(1-\Phi)^x}{\sqrt{5}} \end{array} [/math]

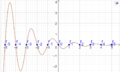
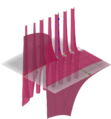
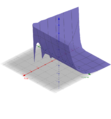
Der Graph dieser Funktion sieht wie folgt aus (Darstellung als Kurve mit Kurvenparameter x):

[math] -5\leq x\leq0[/math]
[math] 0\leq x\leq5[/math]

Eine andere Darstellung sieht wie Folgt aus:

Realteil der Moivre-Binet-Funktion
Imaginärteil der Moivre-Binet-Funktion

Kompexe Fibonacci-Funktion

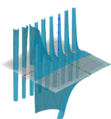
Wir haben bereits gesehen, dass wir die Fibonaccifolge auf eine komplexwertige Funktion mit reellen Eingabewerten erweitern können. Nun können wir dieses Konzept noch weiter abstrahieren, indem wir auch komplexe Eingabewerte zulassen:

[math] \begin{array}{rl} f:&\mathbb{C}\to\mathbb{C}\\&x\mapsto f(z)=\frac{\Phi^z-(1-\Phi)^z}{\sqrt{5}} \end{array} [/math]

Zugegeben, dies hat nun nicht mehr viel mit der ursprünglichen Fibonacci-Folge als Folge natürlicher Zahlen zu tun. Da die Darstellung komplexer Funktionen immer etwas kompliziert ist, zeigen wir mehrere Darstellungsmöglichkeiten:

Darstellung mittels Domain colouring

Mit Geogebra (Bemerkung: Da Geogebra keine sonderlich exakte Berechnung ermöglicht, sind diese Bilder etwas ungenauer):

Realteil
Imaginärteil
Betrag

Interaktive Darstellung mittels Geogebra:

https://www.geogebra.org/m/qhrggvtr

Nullstellen

Wie man bereits anhand der Bilder (mehr oder weniger gut) erkennen kann, liegen alle Nullstellen auf einer Gerade durch den Nullpunkt. Genauer lassen sich alle Nullstellen [math]z_0[/math] darstellen als:

[math]z_0=n\cdot\frac{2\pi}{\ln(\Phi)-\ln(1-\Phi)}\qquad n\in\mathbb{Z}[/math]

Beweis
. Es gilt: [math] \begin{array}{rcll} f(z)=\frac{\Phi^z-(1-\Phi)^z}{\sqrt{5}}&=&0&\\ \Phi^z&=&(1-\Phi)^z&\\ z\cdot\ln(\Phi)&=&z\cdot\ln(1-\Phi)+2\pi n&\qquad n\in\mathbb{Z}\\ z&=&n\cdot\frac{2\pi}{\ln(\Phi)-\ln(1-\Phi)}&\qquad n\in\mathbb{Z} \end{array} [/math]