Zufallsmatrizen - Bohemians und die geheimnisvolle Ordnung im Chaos
Hier entsteht eine tolle Seite ... bis dahin noch etwas Geduld! :D
Einleitung
"Zufallsmatrix" - eine Matrix mit zufälligen Einträgen - klingt zuerst einmal vielleicht nach etwas Willkürlichem und nicht besonders spannend. Wie daraus solche faszinierenden Bilder entstehen, was man sonst noch alles damit anstellen kann und welche Möglichkeiten sich für die Forschung in der Physik und anderen Wissenschaften ergeben, soll in diesem Artikel gezeigt werden.
Zufallsmatrizen
Definition
Eine Zufallsmatrix ist eine Matrix, deren Einträge teils oder ganz zufällig sind.
Universelle Eigenschaften
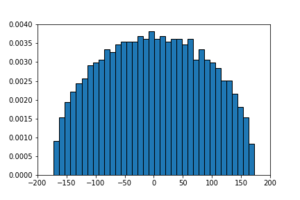
Es gibt offensichtlich sehr viele Methoden solche Matrizen auszuwählen, dabei kann die Wahrscheinlichkeitsverteilung, die Menge, aus der man die Einträge nimmt oder die Symmetrie der Matrizen sehr stark variieren. Wir betrachten nun symmetrische Matrizen, deren Einträge unabhängig voneinander gemäß der Normalverteilung ausgewählt sind. Für den Grenzfall von unendlicher Größe ergeben die Eigenwertabstände dieser Matrizen eine Kurve. Die Klasse der Zufallsmatrizen, deren Eigenwertabstände dieser Kurve folgen, nennt man gaußsches orthogonales Ensemble (GOE). Die Verteilung der Eigenwerte, die bei einer symmetrischen Matrix rein reell sind, nähert sich dabei für sehr große Matrizen einem Halbkreis an:
Analog ergeben Eigenwertabstände hermiteschen Zufallsmatrizen eine andere Kurve, diese Klasse nennt man gaußsche unitäre Ensemble (GUE). (eine hermitesche Matrix ist eine symmetrische Matrix mit komplexen Einträgen und bei der Spiegelung wird das Vorzeichen des Imaginärteils gedreht:
[math]\begin{pmatrix} 1 & 2 & 3+i \\ 2 & 5 & 6-2i \\ 3-i & 6+2i & 7 \end{pmatrix}[/math]
Diese gehören zu den sogenannten Wigner-Verteilungen, benannt nach dem Physiker Eugene Wigner, der in den 1950er bei der Analyse von schweren Atomkernen auf diese Verteilungen stieß. Diese Entdeckungen erweckten allgemeine wissenschaftliche Interesse an Zufallsmatrizen und an deren Eigenschaften. Seitdem wurden viele weitere Familien von Zufallsmatrizen untersucht und dabei andere Ensembles entdeckt, deren Eigenwertabstände andere Kurven folgen. Man fand dabei heraus, dass diese Eigenwertabstände nicht von der Wahrscheinlichkeitsverteilung der Einträge abhängig sind, sondern nur von den Symmetrien der entsprechenden Matrizen. Der Grund dafür ist der extreme Größe der Matrizen. Dann heben sich nämlich die verwirrende Effekte der Funktion zur Eigenwertberechnung im Mittel auf, und die Funktion strebt gegen einen Durchschnittswert. Allerdings lassen sich diese universelle Eigenschaften schwer beweisen und bis heute gibt es noch viele offene Probleme in diesem Teilgebiet.
Nicht universelle Eigenschaften
Zufallsmatrizen haben allerdings nicht nur universelle Eigenschaften (die, die nicht von der Wahrscheinlichkeitsverteilung abhängen) so eine ist zum Beispiel die Dichte von Eigenwerten.
| [math] \frac{N_{f,H} - \int f(\lambda) \, dN(\lambda)}{\sigma_{f, n}} \overset{D}{\longrightarrow} N(0, 1) [/math] |
Anwendungsgebiete
Mehr dazu in "Trivia"
Bildverarbeitung
1.2.2 Image Processing https://math.uni.lu/eml/projects/reports/random-matrices.pdf
Although Wigner’s random matrices have had a huge impact on quantum mechanic problems, there are also concrete applications of random matrix theory in our everyday life, for example image processing. There is a connection with random matrix theory and image denoising filters: Image noise is a random variation of brightness or color information in images, and it is an undesirable by-product of an image capture, which obscures the desired information.
Originally ”noise” denotes ”unwanted signal” and there exist many di↵erent types of ”noise” inter alia ”Gaussian noise”, which is caused by poor illumination, poor transmission or high temperature during a digital image acquisition. Gaussian noise is additive and independent of the signal at each pixel neighbourhood.
We assume that each local matrix associated to these pixels is random and since the eigenvalue density of a random matrix is known, this provides a large threshold for removing the additive Gaussian random noise in the capture, while preserving the main information of the image. To put it in a nutshell, the goal is to compute the eigenvalue density for each local random matrix and find out at which scale the eigenvalue changes from the original image to the noisy counterpart. Hence, by solving the inverse problem, one can free images from unwanted Gaussian noise.
Zufallsmatrizen sind jedem von uns sicherlich schon einmal in einem ihrer praktischen Anwendungsgebiete begegnet: Der digitalen Bildverarbeitung.
Bei der Aufnahme von Fotos begegnet man oft dem sogenannten Bildrauschen, bei dem ein Bild störende Pixel aufweist, die in Farbe und Helligkeit deutlich von eigentlichen Bild abweichen. Dies tritt vor allem bei einer schlechten Belichtungssituation, wie während der Dämmerung oder nachts, auf.
Quantenmechanik/Physik
Text einfügen?
| Trallala |
|---|
| Test |
Bohemian Matrices
Bohemian Matrices sind eine bestimmte Form von Zufallsmatrizen. Eine Familie von Bohemian Matrices ist eine Verteilung von kleinen bis etwa 20x20 dimensionalen Zufallsmatrizen, deren Einträge auf eine (diskrete) Menge ganzer Zahlen (aus einem endlichen Intervall) beschränkt sind, wie z. B. [math]\{-1, 0, 1\}[/math]. (Die ausgewählten Zahlen sind dabei unabhängig von der Dimension der Matrix). Zusätzlich kann eine bestimmte Struktur der Matrix vorgegeben werden (z.B. Diagonalmatrix, Dreiecksmatrix etc.). Der Name "Bohemian" steht dabei für "bounded height integer matrix eigenvalues", woraus aus der Abkürzung BHIME dann Bohemian wurde. Das Feld der Bohemian Matrices umfasst mittlerweile auch Matrizen mit Einträgen aus kontinuierlichen bzw. nicht-endlichen Mengen, obwohl diese nach dieser Namensgebung streng genommen nicht mit inbegriffen wären.
Ihre Untersuchung ist ein recht neues und noch unentdecktes Forschungsgebiet und wird bislang im Rahmen der angewandten Mathematik betrachtet. Betrachtet werden dabei bspw. die Verteilung der Eigenwerte, ihre Symmetrien und Zahlenfolgen, die sich aus ihren Eigenschaften ergeben. Diese weisen oft (überraschende) Querverbindungen mit anderen Bereichen der Mathematik auf.
Wie macht man daraus Bilder?
Um die Eigenwerte der Zufallsmatrizen zu visualisieren, wird zunächst ein Satz von Matrizen nach dem gewünschten Muster generiert. Die Anzahl liegt dabei meist zwischen [math] 10^6[/math] und [math]10^7[/math], bei nur schwach zu sehenden Mustern müssen aber teilweise auch mehr Matrizen einberechnet werden, um ein besseres Bild zu erhalten.
Von diesen Matrizen werden dann die Eigenwerte und deren Dichte berechnet, das heißt je häufiger ein Eigenwert in den Matrizen vorkommt, desto stärker fällt dieser ins Gewicht.
Real- und Imaginärteil dieser Dichte werden dann in der komplexen Zahlenebene aufgetragen, wobei die Farbe nach einem vorher festgelegten Farbschema anhand der Dichte festgelegt wird.
Der Code zum Berechnen der Bilder ist frei verfügbar für Python: https://github.com/BohemianMatrices/bohemian-python und Matlab: https://github.com/BohemianMatrices/BHIME-Project . Die Bilder in diesem Artikel wurden in Matlab generiert.
Galerie
Je nachdem, wie man die Einträge und die Struktur einer Zufallsmatrix auswählt, kommen bei der Betrachtung der Eigenwertdichte unterschiedliche Muster und Formen zustande. In dieser Galerie sollen einige davon mit den zugehörigen Bildern vorgestellt werden. Es handelt sich bei allen Bildern um unsere Eigenkreationen (no pun intended).
Zufällige Matrix mit Einträgen aus diskreter Menge
Die wohl einfachste Art von Zufallsmatrizen sind [math]n\times n[/math] Matrizen, bei denen jeder Eintrag zufällig aus einer endlichen Menge von vorher festgelegten Werten ausgewählt wird. Von der so gewählten Matrix werden nun die Eigenwerte berechnet. Diese liegen in der komplexen Ebene, von welcher man einen Ausschnitt als Bild darstellt. Dabei entstehen Muster mit annähernd fraktal aussehenden Strukturen entlang der reellen Achse.
Eigenwertdichte von 10 Millionen [math]6 \times 6[/math] Matrizen mit Einträgen aus der Menge [math] \{-1, -\frac{1}{1000}, 0, \frac{1}{1000}, 1\} [/math]
Zoom in die Mitte des Bildes im Abschnitt Einleitung
"Eigenkäfer" - Eigenwertdichte von 10 Millionen [math]6 \times 6[/math]Matrizen mit Einträgen aus der Menge [math] \{-1, -\frac{1}{100}, 0, \frac{1}{1000}, 12\} [/math]
Betaverteilung
Bei diesen Matrizen werden alle Einträge zufällig aus einer Betaverteilung mit vorher festgelegten Parametern generiert. Zusätzlich wird eine Amplitude und Verschiebung hinzugefügt, sodass die Einträge von der Form [math]A*x+b[/math] sind, wobei x der Wert aus der Betaverteilung ist. Dadurch entstehen je nach Wahl der Parameter Linienmuster, auf denen sich die Eigenwerte häufen.
Eigenwertdichte von 15 Millionen [math]6\times 6[/math] Matrizen mit Werten aus einer Betaverteilung mit den Parametern [math] \alpha = 0{,}001, \: \beta = 0{,}001 [/math] (Die Eigenwerte wurden an der imaginären Achse gespiegelt)
Eigenwertdichte von 5 Millionen [math]3\times 3[/math] Matrizen mit Werten aus einer Betaverteilung mit den Parametern [math] \alpha = 0{,}01, \: \beta = 0{,}01, \: A=5, \: b=-0{,}5[/math], (Die Eigenwerte wurden an der imaginären Achse gespiegelt)
Eigenwertdichte von 30 Millionen [math]6\times 6[/math] Matrizen mit Werten aus einer Betaverteilung mit den Parametern [math] \alpha = 0{,}001, \: \beta = 0{,}01, \: A=5, \: b=-2 [/math] (Die Eigenwerte wurden an der imaginären Achse gespiegelt)
Obere Hessenbergmatrix
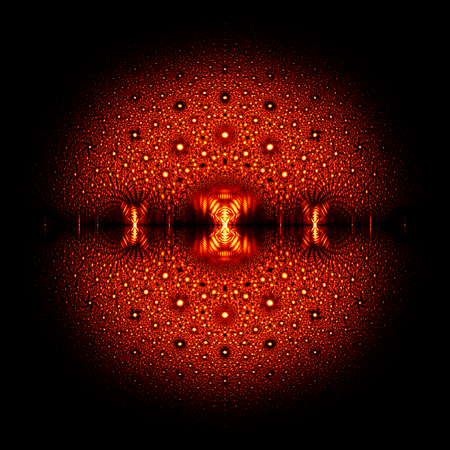
Eine obere Hessenbergmatrix ist ähnlich wie eine obere Dreiecksmatrix, nur dass diese auch Einträge auf der ersten Nebendiagonalen unter der Hauptdiagonalen besitzt. Beispielsweise ist [math]\begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 0 & 9 & 10 & 11 \\ 0 & 0 & 12 & 13 \end{pmatrix}[/math]eine obere Hessenbergmatrix. Analog ist [math]\begin{pmatrix} 1 & 2 & 0 & 0 \\ 3 & 4 & 5 & 0 \\ 6 & 7 & 8 & 9 \\ 10 & 11 & 12 & 13 \end{pmatrix}[/math]eine untere Hessenbergmatrix.
Eigenwertdichte von 20 Millionen [math]12 \times 12[/math] oberer Hessenbergmatrizen mit Toeplitz-Struktur und Einträgen aus der Menge [math]\{-1, 0, 1\}[/math]
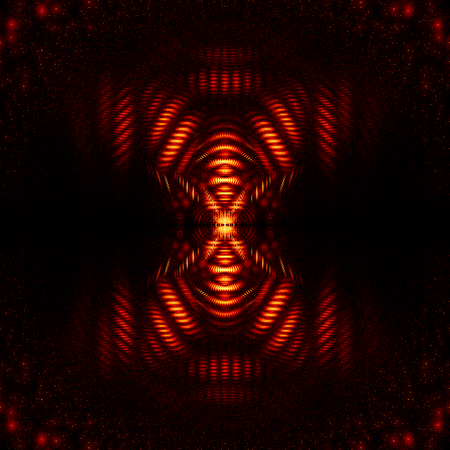
Tridiagonalmatrix
Eine Tridiagonalmatrix ist sowohl eine obere als auch eine untere Hessenbergmatrix und hat somit nur Einträge auf der Hauptdiagonalen und den beiden angrenzenden Nebendiagonalen. Z.B.:[math]\begin{pmatrix} 1 & 2 & 0 & 0 \\ 3 & 4 & 5 & 0 \\ 0 & 6 & 7 & 8 \\ 0 & 0 & 9 & 10 \end{pmatrix}[/math]
Eigenwertdichte von 10 Millionen [math]10 \times 10[/math] Tridiagonalmatrizen mit Einträgen aus der Menge [math]\{-π, π\}[/math]
Feste Matrix mit kontinuierlicher Verteilung in bestimmten Werten (Eigenfish)
Hier wurden Matrizen von der Form
[math]\begin{pmatrix} 0 & 0 & 0 & A \\ -1 & -1 & 0 & 0 \\ B & 0 & 0 & 0 \\ -1 & 1 & 1 & -1 \end{pmatrix}[/math]
verwendet. Die Einträge A und B wurden dabei zufällig aus einem kontinuierlichen Intervall ausgewählt.
Eigenwertdichte von 3 Millionen Matrizen mit [math]A,B \in [][/math]
Eigenwertdichte von 3 Millionen Matrizen mit [math]A,B \in [][/math]
Trivia
Zufallsmatrizen können in den unterschiedlichsten, teils überraschenden Themengebieten genutzt werden, um (Natur-)Phänomene zu beschreiben oder Daten zu modellieren. So etwa bei:
- Abständen parkender Autos und von Bäumen im Urwald
- Verknüpfung von Neuronen im Gehirn
- Datenkompression, Mobilfunk
- Finanzwirtschaft (Fluktuation von Börsenkursen)
- der Statistik ankommender U-Bahnen in New York
Warum genau es so gut funktioniert, diese doch sehr unterschiedlichen Dinge treffend durch Zufallsmatrizen zu beschreiben, ist überwiegend unbekannt.
Nicht nur in praktischen Anwendungsgebieten werden Zufallsmatrizen benutzt: Auch bei theoretischeren Problemen in der Mathematik, wie dem Beweis der Riemannschen Vermutung, sind Zufallsmatrizen möglicherweise ein vielversprechender Ansatz, zu einer Lösung zu gelangen, bspw. über eine Matrix, von den Wissenschaftlern Riemannium getauft, deren Eigenwerte den Nullstellen der Riemannschen Zeta-Funktion entsprechen.
Auch Fraktale wie Julia- und Mandelbrotmengen tauchen im Zusammenhang mit Zufallsmatrizen auf.
Quellen und Links
Quellen