Die Keplerschen Gesetze und das Zweikörperproblem
Geschichte der Gesetze
Beweis der Gesetze
Voraussetzung
Kepler versuchte Gesetze zu formen, die die Planetenbewegung beschreiben. Seine Überlegungen gingen von einem heliozentrische Weltbild, auch Kopernikanisches Weltbild genannt, aus. Hierbei gilt die Sonne als fixes Zentrum des Universums und die Planeten bewegen sich um sie herum. Mit Hilfe von Beobachtungswerten, vor allem der Marsbahn, schloss er, dass die Planeten sich nicht auf idealen Kreisbahnen bewegen. Seine Gesetze sind folglich empirisch. Ihre Gültigkeit lässt sich jedoch mit heutigen Wissen belegen
Das erste Gesetz (Ellipsensatz) lässt sich mittels der Clairautschen Differentialgleichung beweisen.
Das zweite Gesetz (Flächensatz) folgt aus der Drehimpulserhaltung.
Das dritte Gesetz lässt sich mittels der Newtonschen Gesetze direkt beweisen.
Erstes Keplersches Gesetz (Ellipsensatz)
Himmelkörper bewegen sich auf elliptischen Umlaufbahnen um das Baryzentrum herum. Das Baryzentrum bildet den gewichteten Massenmittelpunkt
mehrerer Massen (Brennpunkte). Im Falle der Planeten unseres Sonnensystems bildet die Sonne einen dieser Brennpunkte. Der andere Brennpunkt ist
leer. Dies ergibt sich aus Newtons Gravitationsgesetz, da die Masse des Zentralkörpers (hier die Sonne) wesentlich größer als die der Planeten ist und
die Wirkung der Planeten auf die Sonne vernachlässigt werden kann.
Herleitung
1. Die Bewegung eines Planeten um einen Zentralkörper unter dem Einfluss der Gravitationskraft verläuft in einer Ebene
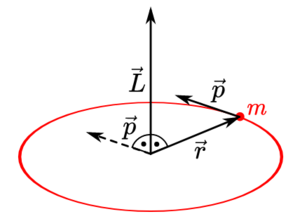
Der Bewegung der Planeten zugrunde liegt der Drehimpuls. Der Drehimpulsvektor [math]\vec{L}[/math] ist definiert als das Kreuzprodukt seines Ortsvektor [math]\vec{r}[/math] und seines Impulsvektor [math]\vec{p}[/math]:
- [math]\vec{L} = \vec{r} \times \vec{p}[/math]
Daraus ergibt sich, dass der Drehimpuls [math]\vec{L}[/math] senkrecht zum Ortsvektor [math]\vec{r}[/math] und zum Impulsvektor [math]\vec{p}[/math] gerichtet ist. Jedoch müssen der Ortsvektor [math]\vec{r}[/math] und der Impulsvektor [math]\vec{p}[/math] nicht notwendigerweise senkrecht zueinander stehen. In der klassischen Mechanik ergibt dich der Impulsvektor [math]\vec{p}[/math] aus dem Produkt der Masse [math]m[/math] des bewegten Körpers und der Geschwindigkeit [math]\vec{v}[/math]. Folglich gilt wegen [math]\vec{p} = m \cdot \vec{v}[/math] für den Drehimpuls:
- [math]\vec{L} = \vec{r} \times \vec{p} = m \cdot (\vec{r} \times \vec{v})[/math]
Bleibt nun der Drehimpuls des bewegten Körpers im Laufe der Zeit konstant, dann liegen Ortsvektor [math]\vec{r}[/math] und Geschwindigkeit [math]\vec{v}[/math] fortwährend in einer gemeinsamen Ebene, in der dann der Körper rotiert. Mit Hilfe der zeitlichen Ableitung des Drehimpulses lässt sich nachweisen, dass bei der Bewegung eines Planeten um einen Zentralkörper unter dem Einfluss der Gravitationskraft der Drehimpuls des Trabanten konstant bleibt.
- [math]\frac{d}{dt}\vec{L} = \frac{d}{dt}(\vec{r} \times \vec{p}) = \frac{d}{dt}(\vec{r} \times m \cdot \vec{v}) = m \cdot \frac{d}{dt}(\vec{r} \times \vec{v}) = m\cdot(\vec{r} \times \vec{a}) = (\vec{r} \times m \cdot \vec{a}) = \vec{r} \times \vec{F}[/math]
Da die Gravitationskraft [math]\vec{F}[/math] auf den Planeten stets in Richtung des Zentralkörpers und somit entgegengesetzt zum Ortsvektor [math]\vec{r}[/math] gerichtet ist, ist das Kreuzprodukt von [math]\vec{r}[/math] und [math]\vec{F}[/math] folglich der Nullvektor [math]\vec{0}[/math]:
- [math]\vec{r} \times \vec{F} = \vec{0}[/math]
Damit ergibt sich:
- [math]\frac{d}{dt}\vec{L} = \vec{r} \times \vec{F} = \vec{0} \Rightarrow \vec{L} = \vec{r} \times \vec{p} = m \cdot (\vec{r} \times \vec{v})\enspace \text{ist konstant}[/math]
Hieraus ergibt sich, dass die Bewegung eines Planeten um einen Zentralkörper unter dem Einfluss der Gravitationskraft in einer Ebene verläuft.
2. Die Bewegung eines Planeten um einen Zentralkörper unter dem Einfluss der Gravitationskraft verläuft auf einer Ellipsenbahn
Periodische Bewegungen, die in einer Ebene stattfinden, beschreibt man am einfachsten durch sogenannte Polarkoordinaten. Es ergibt sich:
- [math] \begin{align*} x &= r \cdot \cos(\varphi)\\ y &= r \cdot \sin(\varphi) \end{align*}[/math]
Daraus lassen sich die Geschwindigkeitskoordinaten [math]v_x = \dot{x}[/math] und [math]v_y = \dot{y}[/math] errechnen. Mit der Winkelgeschwindigkeit [math]\omega = \dot{\varphi}[/math] ergibt sich:
- [math] \begin{align*} \dot{x} &= \dot{r} \cdot \cos(\varphi) - r \cdot \sin(\varphi) \cdot \omega\\ \dot{y} &= \dot{r} \cdot \cos(\varphi) + r \cdot \cos(\varphi) \cdot \omega\\ \end{align*}[/math]
Die Gesamtenergie [math]E_{ges}[/math] eines Planeten bei der Bewegung um einen Zentralkörper lässt sich durch Polarkoordinaten ausdrücken. Hierfür nutzen wir folgendes:
- [math]m =[/math] Masse des Planeten. [math]M =[/math] Masse des Zentralkörpers.
- Als Radius [math]r[/math] aus dem Term für die potenzielle Energie verwenden wir die Polarkoordinate [math]r[/math].
- Das Geschwindigkeitsquadrat [math]v^2 = v^{2}_x + v^{2}_y[/math] aus der kinetischen Energie schreibt sich in Polarkoordinaten [math]v^2 = \dot{r}^{2} + r^2 \cdot \omega^{2}\enspace \enspace [/math] (1).
- Der Drehimpuls [math]\vec{L}[/math] hat den konstanten Betrag [math]L=m \cdot r^2\cdot \omega\enspace \enspace [/math] (2).
- Aus [math]L = m \cdot \omega \Leftrightarrow \omega = \frac{L}{m \cdot r^2}\enspace \enspace [/math](3).
- [math] \begin{align*}E_{ges} &= E_{kin} + E_{pot}\\ &= \frac{1}{2} \cdot m\cdot v^2 - \frac{G \cdot m \cdot M}{r}\\ &\stackrel{\text{(1)}}{=} \frac{1}{2} \cdot m\cdot (\dot{r}^{2} + r^2 \cdot \omega^{2}) - \frac{G \cdot m \cdot M}{r}\\ &\stackrel{\text{(2)}}{=} \frac{1}{2} \cdot \left(m\cdot \dot{r}^{2} + \frac{L}{m \cdot r^2}\right) - \frac{G \cdot m \cdot M}{r}\\ &\stackrel{\text{(3)}}{=} \frac{1}{2} \cdot \left(\frac{L}{m \cdot r^4}\left(\frac{dr}{\varphi}\right)^2 + \frac{L}{m \cdot r^2}\right) - \frac{G \cdot m \cdot M}{r} \end{align*}[/math]
Aufgelöst nach [math]\frac{dr}{d\varphi}[/math] erhält man aus der Gleichung:
- [math]\frac{dr}{d\varphi}=\frac{m\cdot r^2}{L}\cdot \sqrt{\frac{2\cdot E_{ges}}{m} + \frac{2\cdot G\cdot M}{r}-\frac{L^2}{m^2\cdot r^2}}[/math]
Nach [math]d\varphi[/math] aufgelöst, erhalten wir:
- [math]d\varphi = \frac{L}{m \cdot r^2}\cdot \frac {1}{\sqrt{\frac{2 \cdot E_{ges}}{m} + \frac{2 \cdot G \cdot M}{r} -1 \frac{L^2}{m^2 \cdot r^2}}}\cdot dr[/math]
Mit Hilfe von Substitution lässt sich die Bewegungsgleichung integrieren, so erhalten wir durch Umformungen und Resubstitution die Polarkoordinatendarstellung eines Kegelschnittes:
- [math]r(\varphi) = \frac{p}{1-\varepsilon \cdot \cos \left(\varphi \right)}[/math]
Nachweis der Ellipsenbahn
Ellipse mit Halbachsen [math]a[/math] und [math]b[/math] sowie dem Abstand [math]e[/math] vom Mittelpunkt zu den Brennpunkten.
Wir betrachten nun eine Ellipse mit der großen Halbachse [math]a := \frac{p}{1 - \varepsilon^2}[/math] (I), der kleinen Halbachse
[math]b := \frac{p}{\sqrt{1-\varepsilon^2}}[/math] (II) und dem Abstand vom Mittelpunkt zu den Brennpunkten [math]e := a\cdot \varepsilon[/math] (III).
Aus (I), (II) und (III) ergibt sich für diese Ellipse
- [math] \begin{align*} a^2 - b^2 &= \left(\frac{p}{1-\varepsilon^2}\right)^2 - \left(\frac{p}{\sqrt{1 - \varepsilon^2}}\right)^2 \\ &= e^2 \enspace \enspace \enspace \enspace \text{(IV)} \end{align*}[/math]
Aus (I) und (II) ergibt sich
- [math] \frac{b^2}{a} = p \enspace \enspace \enspace \enspace \text{(V)}[/math]
Aus (III) ergibt sich
- [math] \varepsilon = \frac{e}{a} \enspace \enspace \enspace \enspace \text{(VI)}[/math]
Aus (V) und (VI) ergibt sich [math] r = \frac{b^2}{a - e \cdot \cos \left(\varphi \right)} \Leftrightarrow a - e \cdot \cos \left(\varphi \right) = \frac{b^2}{r} \Leftrightarrow e\cdot \cos \left(\varphi \right) = a - \frac{b^2}{r} \enspace \enspace \enspace \enspace \text{(VII)}[/math]
Der Abstand der beiden Brennpunkte, den wir zuvor mit [math]2 \cdot e[/math] angegeben haben, lässt sich nun als [math]r \cdot \cos \left(\varphi \right)[/math] und [math]2e - r \cdot \cos \left(\varphi \right)[/math] schreiben. Daraus ergibt sich nun eine Ellipse mit den Strecken [math]r[/math] und [math]s[/math]. Die beiden Dreiecke lassen sich mit Hilfe des Satzes von Pythagoras berechnen. Für das Dreieck mit der Hypotenuse [math]r[/math] gilt:
- [math] r^2 = (r\cdot \cos \left(\varphi \right))^2 + x^2 \Leftrightarrow x^2 = r^2 - r^2 \cdot \cos^2 \left(\varphi \right) \enspace \enspace \enspace \enspace \text{(VIII)}[/math]
Für das Dreieck mit der Hypotenuse $s$ gilt:
- [math] s^2 = x^2+(2 \cdot e-r \cdot \cos \left(\varphi \right))^2 [/math]
Nehmen wir nun diese Gleichung und wenden (VIII), (IV) und (VII) darauf an, so erhalten wir:
- [math] \begin{align*} s^2 & \stackrel{\hphantom{\text{(IV),(VII)}}}{=} x^2+(2 \cdot e-r \cdot \cos \left(\varphi \right))^2 \\ & \stackrel{\hphantom{\text{(.)}}\text{(VIII)}\hphantom{\text{(.)}}}{=} 4\cdot e^2-4\cdot e\cdot r\cdot \cos \left(\varphi \right)+r^2\\ & \stackrel{\text{(IV),(VII)}}{=} (2\cdot a-r)^2 \end{align*}[/math]
Somit ergibt dich die Gleichung
- [math] s=2\cdot a-r [/math]
und wir erhalten
- [math] r+s = r+2\cdot a -r = 2\cdot a \text{ ist konstant}[/math]
Hieraus folgt, da die Summe der Streckenlängen [math]r[/math] und [math]s[/math] konstant ist, bewegt sich der Körper der Definition nach auf einer Ellipse.
Zweites Keplersches Gesetz (Flächensatz)
In gleichen Zeiten überstreicht der Fahrstrahl Objekt-Gravizentrum gleiche Flächen.
Der Fahrstrahl bildet die Verbindungslinie zwischen dem Schwerpunkt eines Himmelskörpers und dem Gravizentrum seiner Bewegung, dem Zentralkörper. Dies ergibt sich aus der Gravitationskraft, die entlang des Fahrstrahls wirkt und aus der Drehimpulserhaltung.
Herleitung
In der Zeit [math]\Delta t[/math] bewegt sich der Himmelskörper von Ort [math]r_1[/math] bis Ort [math]r_2[/math], hierbei überstreicht der Fahrstrahl eine Fläche [math]A[/math]. Diese Fläche besitzt bei ausreichend kleiner [math]\Delta t[/math] die Form eines Dreiecks, das von [math]r_1[/math], [math]r_2[/math] und dem Wegstück [math]s=v\cdot \Delta t[/math] begrenzt ist. Für die Fläche A gilt:
- [math] A=\frac{1}{2}\cdot r\cdot h = \text{const.} \text{ mit } h=\sin\left(\alpha\right)\cdot v\cdot\Delta t,[/math]
wobei [math]\alpha[/math] der Winkel zwischen Radiusvektor und Geschwindigkeitsvektor ist. Daraus ergibt sich:
- [math] A=\frac{1}{2}\cdot r\cdot \sin\left(\alpha\right)\cdot v\cdot\Delta t=\text{const.}[/math]
Da [math]\frac{1}{2}[/math] und [math]\Delta t[/math] gleich bleiben, lassen sie sich raus kürzen und es ergibt sich
- [math] A=r\cdot \sin\left(\alpha\right)\cdot v=\text{const.}[/math]
Geschwindigkeitsverhältnis von Perihel und Aphel
Als Perizentrum und Apozentrum werden die beiden Brennpunkte des Baryzentrums bezeichnet, hierbei bildet die Sonne das Perizentrum. Die beiden Punkte, an der Himmelskörper den Brennpunkten am nächsten sind, bilden die Schnittpunkte der Umlaufbahn mit der Linie durch die beiden Brennpunkte. Hierbei bezeichnet Perihel den dem Perizentrum nächsten, sonnennächsten Punkt und Aphel den dem Apozentrum nächsten Punkt. Die Erde erreicht diese Punkte Anfang Januar (Prihel) mit ca. 147,1 Mio. km bzw. 0,983 AE und Anfang Juli (Aphel) mit ca. 152,1 Mio. km bzw. 1,017 AE Entfernung zur Sonne. Da das Produkt [math]r\cdot v\cdot\sin\left(\alpha\right)[/math] konstant ist und an den Punkten Perihel und Aphel [math]\alpha=90^\circ[/math], daraus folgt [math]sin\left(\alpha\right)=1[/math]. Somit stehen Perihel und Aphel in folgender Beziehung:
- [math]r_{Aphel}\cdot v_{Aphel}=r_{Perihel}\cdot v_{Perihel} \geq (a+e)\cdot v_{Aphel} = (a-e)\cdot v_{Perihel}[/math]
Der Zentalkörper und der Himmelskörper bilden ein geschlossenes System, in dem sich der Drehimpuls nicht ändern darf. Daraus ergibt sich, dass der Himmelskörper eine geringere Geschwindigkeit hat, wenn dieser weit weg vom Drehpunkt ist. Je näher er dem Drehpunkt kommt, desto größer ist seine Geschwindigkeit. Dem Drehimpulserhaltungssatz nach ist:
- [math] m\cdot v\cdot r\cdot \sin\left(\alpha\right)=\text{const.}[/math]
Wegen der konstanten Masse folgt
- [math] v\cdot r\cdot \sin\left(\alpha\right)=\text{const.}[/math]
Dies entspricht der Konstanz der überstrichenen Flächen im zweiten Keplerschen Gesetz.
Drittes Keplersches Gesetz
Die Quadrate der Umlaufzeiten stehen im gleichen Verhältnis wie die Kuben (dritten Potenzen) der großen Halbachsen, hierbei ist [math]T=\Delta t[/math]:
- [math] \left({\frac {T_{1}}{T_{2}}}\right)^{2}=\left({\frac {r_{1}}{r_{2}}}\right)^{3}[/math]
Herleitung
Aus dem Gravitationsgesetz lässt sich herleiten, dass für alle Planeten im Gravitationsfeld der Sonne der Quotient aus der dritten Potenz des Kreisradius und dem Quadrat der Umlaufzeit gleich groß und damit für das gesamte Planetensystem konstant ist. Entlang des Radius [math]r[/math] wirkt die Zentripetalkraft [math]F_Z[/math] des Zentralkörpers.
- [math] F_Z= F_G \Leftrightarrow m\cdot a_Z=G\cdot \frac{m\cdot M}{r^2}[/math]
Mit der Winkelgeschwindigkeit [math]\omega=\frac{v}{r} \Leftrightarrow v=r \cdot \omega[/math] ergibt sich:
- [math] \begin{align*} G\cdot \frac{m\cdot M}{r^2}&=m\cdot a_z\\ &=m\cdot \frac{v^2}{r}\\ &=m\cdot \frac{r^2\cdot \omega^2}{r}\\ &=m\cdot r\cdot \omega^2 \end{align*}[/math]
Aufgrund der konstanten Winkelgeschwindigkeit gilt:
- [math] \omega = \frac{2\pi}{T}[/math]
Damit ergibt sich:
- [math] m\cdot r \cdot \frac{4\pi^2}{T^2}=G\cdot \frac{m\cdot M}{r^2} \Leftrightarrow r\cdot \frac{4\pi^2}{T^2}=G\cdot \frac{M}{r^2} \Leftrightarrow \frac{r^3}{T^2}=G\cdot \frac{M}{4\pi^2}[/math]
Da nun [math]\frac{r^3}{T^2}=G\cdot \frac{M}{4\pi^2}[/math] nicht mehr abhängig von [math]m[/math] der Masse des bewegten Körpers ist, sondern nur noch von [math]M[/math] der Masse des Zentralkörpers, gilt für Planeten, die um den selben Zentralkörper bewegen (für die [math]M[/math] identisch ist):
- [math] \frac{r^3}{T^2}=\text{const.}[/math]
Daraus folgt:
- [math] \begin{align*} \frac{r_1^3}{T_1^2} &= \frac{r_2^3}{T_2^2}\\ T_1^2\cdot r_2^3 &= T_2^2\cdot r_1^3\\ \left({\frac {T_{1}}{T_{2}}}\right)^{2}&=\left({\frac {r_{1}}{r_{2}}}\right)^{3} \end{align*}[/math]