Fibonacci Folge: Unterschied zwischen den Versionen
| Zeile 16: | Zeile 16: | ||
\end{array} \cdots </math> | \end{array} \cdots </math> | ||
| + | Die Beträge der Werte sind symmetrisch, im Negativen alternieren sie jedoch. Dementsprechend nähert sich das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen im Negativen gegen <math>-\frac{1}{\Phi}</math> an. | ||
==Kontinuierliche Fibonacci-Funktion== | ==Kontinuierliche Fibonacci-Funktion== | ||
| Zeile 23: | Zeile 24: | ||
<math> f_n=\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}</math> | <math> f_n=\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}</math> | ||
| − | <math>\Phi</math> ist dabei | + | <math>\Phi</math> ist dabei der [[goldener Schnitt]] <math>\Phi=\frac{1+\sqrt{5}}{2}</math>. Diese Formel liefert für ganzzahlige Werte für n auch exakte, ganzzahlige Ergebnisse. |
{| class="wikitable left mw-collapsible mw-collapsed font-size: 105.3%;" | {| class="wikitable left mw-collapsible mw-collapsed font-size: 105.3%;" | ||
| − | |style="text-align:left; font-size: 95%;"| '''Beweis durch vollständige Induktion''' | + | | style="text-align:left; font-size: 95%;" | '''Beweis durch vollständige Induktion''' |
|- | |- | ||
|. | |. | ||
| Zeile 32: | Zeile 33: | ||
Um zu zeigen, dass diese Formel die Fibonacci-Zahlen ergibt, überprüfen wir die Bildungsvorschrift: | Um zu zeigen, dass diese Formel die Fibonacci-Zahlen ergibt, überprüfen wir die Bildungsvorschrift: | ||
| − | '''IA''': Die Formel gilt für <math>n=0\ \left(\frac{\Phi^0-(1-\Phi)^0}{\sqrt{5}}=\frac{1-1}{sqrt{5}}=0=f_0\right)</math> und für <math> n=1\ \left( f_1= \frac{\Phi^1-(1-\Phi)^1}{\sqrt{5}}=\frac{\sqrt{5}}{sqrt{5}}=1=f_1\right)</math>. | + | '''IA''': Die Formel gilt für <math>n=0\ \left(\frac{\Phi^0-(1-\Phi)^0}{\sqrt{5}}=\frac{1-1}{\sqrt{5}}=0=f_0\right)</math> und für <math> n=1\ \left( f_1= \frac{\Phi^1-(1-\Phi)^1}{\sqrt{5}}=\frac{\sqrt{5}}{\sqrt{5}}=1=f_1\right)</math>. |
'''IV''': Nun gelte sie für ein <math> n,\ n-1\in\mathbb{N}</math>. | '''IV''': Nun gelte sie für ein <math> n,\ n-1\in\mathbb{N}</math>. | ||
| Zeile 40: | Zeile 41: | ||
<math> | <math> | ||
\begin{array}{rl} | \begin{array}{rl} | ||
| − | f_{n+1}=f_{n}+f_{n | + | f_{n+1}=f_{n}+f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n+\Phi^{n-1}-(1-\Phi)^{n-1}}{\sqrt{5}}\\ |
&=\frac{\Phi^{n-1}(1+\Phi)-(1-\Phi)^{n-1}\left(1+(1-\Phi)\right)}{\sqrt{5}}\\ | &=\frac{\Phi^{n-1}(1+\Phi)-(1-\Phi)^{n-1}\left(1+(1-\Phi)\right)}{\sqrt{5}}\\ | ||
&=\frac{\Phi^{n-1}(\Phi^2)-(1-\Phi)^{n-1}(1-\Phi)^2}{\sqrt{5}}\\ | &=\frac{\Phi^{n-1}(\Phi^2)-(1-\Phi)^{n-1}(1-\Phi)^2}{\sqrt{5}}\\ | ||
&=\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\sqrt{5}} | &=\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\sqrt{5}} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | Ebenso für negative Zahlen: | ||
| + | |||
| + | <math> | ||
| + | \begin{array}{rl} | ||
| + | f_{n-2}=f_{n}-f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n-\Phi^{n-1}+(1-\Phi)^{n-1}}{\sqrt{5}}\\ | ||
| + | &=\frac{\Phi^{n-1}(\Phi-1)-(1-\Phi)^{n-1}\left((1-\Phi)-1\right)}{\sqrt{5}}\\ | ||
| + | &=\frac{\Phi^{n-1}\left(\frac{1}{\Phi}\right)-(1-\Phi)^{n-1}\left(\frac{1}{1-\Phi}\right)}{\sqrt{5}}\\ | ||
| + | &=\frac{\Phi^{n-2}-(1-\Phi)^{n-2}}{\sqrt{5}} | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 49: | Zeile 61: | ||
===Erweiterung auf eine kontinuierliche Funktion=== | ===Erweiterung auf eine kontinuierliche Funktion=== | ||
| − | Nun | + | Nun stellt sich die Frage, was passiert, wenn wir in die Formel von Moivre-Binet nicht-ganzzahlige Werte für n einsetzen, die Fibonacci-Folge also in eine kontinuierliche Funktion umwandeln. Da <math>1-\Phi</math> jedoch negativ ist, und nicht-ganzzahlige Potenzen von negativen Zahlen nur im Komplexen definiert sind, müssen wir den Wertebereich auf <math>\mathbb{C}</math> erweitern: |
| + | [[Datei:Binet1 (1).png|mini]] | ||
| + | <math> | ||
| + | \begin{array}{rl} | ||
| + | f:&\mathbb{R}\to\mathbb{C}\\&x\mapsto f(x)=\frac{\Phi^x-(1-\Phi)^x}{\sqrt{5}} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | [[Datei:Binet1.png|links|mini|<nowiki><math>-5\leq x\leq0</math></nowiki>]] | ||
| + | Der Graph dieser Funktion sieht wie folgt aus (Darstellung als Kurve mit Kurvenparameter x): | ||
Version vom 11. März 2021, 12:36 Uhr
Die Fibonacci-Folge ist eine Folge reeller Zahlen.
Erweiterung auf ganze Zahlen
Die Bildungsvorschrift lässt sich einfach umstellen:
[math] f_{n}=f_{n+2}-f_{n+1} [/math]
Damit erhält man eine erweiterte Fibonacci-Folge:
[math] \cdots\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} f_{-7} & f_{-6} & f_{-5} & f_{-4} & f_{-3} & f_{-2} & f_{-1} & f_0 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7\\\hline 13 & -8 & 5 & -3 & 2 & -1 & 1 & 0 & 1 & 1 & 2 & 3 & 5 & 8 & 13 \end{array} \cdots [/math]
Die Beträge der Werte sind symmetrisch, im Negativen alternieren sie jedoch. Dementsprechend nähert sich das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen im Negativen gegen [math]-\frac{1}{\Phi}[/math] an.
Kontinuierliche Fibonacci-Funktion
Formel von Moivre-Binet
Die Formel von Moivre und Binet ist eine Formel zur expliziten Berechung der n-ten Fibonacci-Zahl:
[math] f_n=\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}[/math]
[math]\Phi[/math] ist dabei der goldener Schnitt [math]\Phi=\frac{1+\sqrt{5}}{2}[/math]. Diese Formel liefert für ganzzahlige Werte für n auch exakte, ganzzahlige Ergebnisse.
| Beweis durch vollständige Induktion |
| .
Um zu zeigen, dass diese Formel die Fibonacci-Zahlen ergibt, überprüfen wir die Bildungsvorschrift: IA: Die Formel gilt für [math]n=0\ \left(\frac{\Phi^0-(1-\Phi)^0}{\sqrt{5}}=\frac{1-1}{\sqrt{5}}=0=f_0\right)[/math] und für [math] n=1\ \left( f_1= \frac{\Phi^1-(1-\Phi)^1}{\sqrt{5}}=\frac{\sqrt{5}}{\sqrt{5}}=1=f_1\right)[/math]. IV: Nun gelte sie für ein [math] n,\ n-1\in\mathbb{N}[/math]. IS: Dann gilt: [math] \begin{array}{rl} f_{n+1}=f_{n}+f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n+\Phi^{n-1}-(1-\Phi)^{n-1}}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(1+\Phi)-(1-\Phi)^{n-1}\left(1+(1-\Phi)\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(\Phi^2)-(1-\Phi)^{n-1}(1-\Phi)^2}{\sqrt{5}}\\ &=\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\sqrt{5}} \end{array} [/math] Ebenso für negative Zahlen: [math] \begin{array}{rl} f_{n-2}=f_{n}-f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n-\Phi^{n-1}+(1-\Phi)^{n-1}}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(\Phi-1)-(1-\Phi)^{n-1}\left((1-\Phi)-1\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}\left(\frac{1}{\Phi}\right)-(1-\Phi)^{n-1}\left(\frac{1}{1-\Phi}\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-2}-(1-\Phi)^{n-2}}{\sqrt{5}} \end{array} [/math] |
Erweiterung auf eine kontinuierliche Funktion
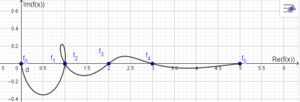
Nun stellt sich die Frage, was passiert, wenn wir in die Formel von Moivre-Binet nicht-ganzzahlige Werte für n einsetzen, die Fibonacci-Folge also in eine kontinuierliche Funktion umwandeln. Da [math]1-\Phi[/math] jedoch negativ ist, und nicht-ganzzahlige Potenzen von negativen Zahlen nur im Komplexen definiert sind, müssen wir den Wertebereich auf [math]\mathbb{C}[/math] erweitern:
[math] \begin{array}{rl} f:&\mathbb{R}\to\mathbb{C}\\&x\mapsto f(x)=\frac{\Phi^x-(1-\Phi)^x}{\sqrt{5}} \end{array} [/math]
Der Graph dieser Funktion sieht wie folgt aus (Darstellung als Kurve mit Kurvenparameter x):