Fibonacci Folge: Unterschied zwischen den Versionen
| Zeile 23: | Zeile 23: | ||
<math> f_n=\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}</math> | <math> f_n=\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}</math> | ||
| + | |||
| + | https://www.geogebra.org/m/wfareu7d | ||
<math>\Phi</math> ist dabei der [[goldener Schnitt]] <math>\Phi=\frac{1+\sqrt{5}}{2}</math>. Diese Formel liefert für ganzzahlige Werte für n auch exakte, ganzzahlige Ergebnisse. | <math>\Phi</math> ist dabei der [[goldener Schnitt]] <math>\Phi=\frac{1+\sqrt{5}}{2}</math>. Diese Formel liefert für ganzzahlige Werte für n auch exakte, ganzzahlige Ergebnisse. | ||
| Zeile 65: | Zeile 67: | ||
<math> | <math> | ||
\begin{array}{rl} | \begin{array}{rl} | ||
| − | f:&\mathbb{R}\to\mathbb{C}\\& | + | f:&\mathbb{R}\to\mathbb{C}\\&z\mapsto f(x)=\frac{\Phi^x-(1-\Phi)^x}{\sqrt{5}} |
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 82: | Zeile 84: | ||
==Kompexe Fibonacci-Funktion== | ==Kompexe Fibonacci-Funktion== | ||
| − | Wir haben bereits gesehen, dass wir die Fibonaccifolge auf eine komplexwertige Funktion mit reellen Eingabewerten erweitern können. Nun können wir dieses Konzept noch weiter abstrahieren, indem wir auch komplexe Eingabewerte zulassen | + | Wir haben bereits gesehen, dass wir die Fibonaccifolge auf eine komplexwertige Funktion mit reellen Eingabewerten erweitern können. Nun können wir dieses Konzept noch weiter abstrahieren, indem wir auch komplexe Eingabewerte zulassen: |
| + | |||
| + | <math> | ||
| + | \begin{array}{rl} | ||
| + | f:&\mathbb{C}\to\mathbb{C}\\&x\mapsto f(z)=\frac{\Phi^z-(1-\Phi)^z}{\sqrt{5}} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | Zugegeben, dies hat nun nicht mehr viel mit der ursprünglichen Fibonacci-Folge als Folge natürlicher Zahlen zu tun. Da die Darstellung komplexer Funktionen immer etwas kompliziert ist, zeigen wir mehrere Darstellungsmöglichkeiten: | ||
<gallery> | <gallery> | ||
Datei:Cmplx binet colour.PNG|Darstellung mittels Domain colouring | Datei:Cmplx binet colour.PNG|Darstellung mittels Domain colouring | ||
</gallery> | </gallery> | ||
| + | |||
| + | Mit Geogebra (Bemerkung: Da Geogebra keine sonderlich exakte Berechnung ermöglicht, sind diese Bilder etwas ungenauer): | ||
| + | <gallery> | ||
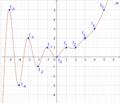
| + | Datei:Realteil_der_komplexen_Moivre-Binet-Formel.png|Realteil | ||
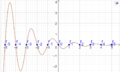
| + | Datei:Imaginärteil_der_komplexen_Moivre-Binet-Formel.png|Imaginärteil | ||
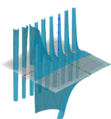
| + | Datei:Betrag_der_komplexen_Moivre-Binet-Formel.png|Betrag | ||
| + | </gallery> | ||
| + | |||
| + | Interaktive Darstellung mittels Geogebra: | ||
| + | |||
| + | https://www.geogebra.org/m/qhrggvtr | ||
| + | |||
| + | ===Nullstellen=== | ||
| + | Wie man bereits anhand der Bilder (mehr oder weniger gut) erkennen kann, liegen alle Nullstellen auf einer Gerade durch den Nullpunkt. Genauer lassen sich alle Nullstellen <math>z_0</math> darstellen als: | ||
| + | |||
| + | <math>z_0=n\cdot\frac{2\pi}{\ln(\Phi)-\ln(1-\Phi)}\qquad n\in\mathbb{Z}</math> | ||
| + | |||
| + | {| class="wikitable left mw-collapsible mw-collapsed font-size: 105.3%;" | ||
| + | | style="text-align:left; font-size: 95%;" | '''Beweis''' | ||
| + | |- | ||
| + | |. | ||
| + | |||
| + | Es gilt: | ||
| + | |||
| + | <math> | ||
| + | \begin{array}{rcll} | ||
| + | f(z)=\frac{\Phi^z-(1-\Phi)^z}{\sqrt{5}}&=&0&\\ | ||
| + | \Phi^z&=&(1-\Phi)^z&\\ | ||
| + | z\cdot\ln(\Phi)&=&z\cdot\ln(1-\Phi)+2\pi n&\qquad n\in\mathbb{Z}\\ | ||
| + | z&=&n\cdot\frac{2\pi}{\ln(\Phi)-\ln(1-\Phi)}&\qquad n\in\mathbb{Z} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | |} | ||
Version vom 11. März 2021, 14:27 Uhr
Die Fibonacci-Folge ist eine Folge reeller Zahlen.
Erweiterung auf ganze Zahlen
Die Bildungsvorschrift lässt sich einfach umstellen:
[math] f_{n}=f_{n+2}-f_{n+1} [/math]
Damit erhält man eine erweiterte Fibonacci-Folge:
[math] \cdots\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} f_{-7} & f_{-6} & f_{-5} & f_{-4} & f_{-3} & f_{-2} & f_{-1} & f_0 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7\\\hline 13 & -8 & 5 & -3 & 2 & -1 & 1 & 0 & 1 & 1 & 2 & 3 & 5 & 8 & 13 \end{array} \cdots [/math]
Die Beträge der Werte sind symmetrisch, im Negativen alternieren sie jedoch. Dementsprechend nähert sich das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen im Negativen gegen [math]-\frac{1}{\Phi}[/math] an.
Kontinuierliche Fibonacci-Funktion
Formel von Moivre-Binet
Die Formel von Moivre und Binet ist eine Formel zur expliziten Berechung der n-ten Fibonacci-Zahl:
[math] f_n=\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}[/math]
https://www.geogebra.org/m/wfareu7d
[math]\Phi[/math] ist dabei der goldener Schnitt [math]\Phi=\frac{1+\sqrt{5}}{2}[/math]. Diese Formel liefert für ganzzahlige Werte für n auch exakte, ganzzahlige Ergebnisse.
| Beweis durch vollständige Induktion |
| .
Um zu zeigen, dass diese Formel die Fibonacci-Zahlen ergibt, überprüfen wir die Bildungsvorschrift: IA: Die Formel gilt für [math]n=0\ \left(\frac{\Phi^0-(1-\Phi)^0}{\sqrt{5}}=\frac{1-1}{\sqrt{5}}=0=f_0\right)[/math] und für [math] n=1\ \left( f_1= \frac{\Phi^1-(1-\Phi)^1}{\sqrt{5}}=\frac{\sqrt{5}}{\sqrt{5}}=1=f_1\right)[/math]. IV: Nun gelte sie für ein [math] n,\ n-1\in\mathbb{N}[/math]. IS: Dann gilt: [math] \begin{array}{rl} f_{n+1}=f_{n}+f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n+\Phi^{n-1}-(1-\Phi)^{n-1}}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(1+\Phi)-(1-\Phi)^{n-1}\left(1+(1-\Phi)\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(\Phi^2)-(1-\Phi)^{n-1}(1-\Phi)^2}{\sqrt{5}}\\ &=\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\sqrt{5}} \end{array} [/math] Ebenso für negative Zahlen: [math] \begin{array}{rl} f_{n-2}=f_{n}-f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n-\Phi^{n-1}+(1-\Phi)^{n-1}}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(\Phi-1)-(1-\Phi)^{n-1}\left((1-\Phi)-1\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}\left(\frac{1}{\Phi}\right)-(1-\Phi)^{n-1}\left(\frac{1}{1-\Phi}\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-2}-(1-\Phi)^{n-2}}{\sqrt{5}} \end{array} [/math] |
Erweiterung auf eine kontinuierliche Funktion
Nun stellt sich die Frage, was passiert, wenn wir in die Formel von Moivre-Binet nicht-ganzzahlige Werte für n einsetzen, die Fibonacci-Folge also in eine kontinuierliche Funktion umwandeln. Da [math]1-\Phi[/math] jedoch negativ ist, und nicht-ganzzahlige Potenzen von negativen Zahlen nur im Komplexen definiert sind, müssen wir den Wertebereich auf [math]\mathbb{C}[/math] erweitern:
[math] \begin{array}{rl} f:&\mathbb{R}\to\mathbb{C}\\&z\mapsto f(x)=\frac{\Phi^x-(1-\Phi)^x}{\sqrt{5}} \end{array} [/math]
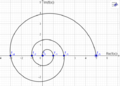
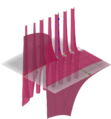
Der Graph dieser Funktion sieht wie folgt aus (Darstellung als Kurve mit Kurvenparameter x):
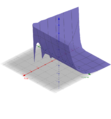
Eine andere Darstellung sieht wie Folgt aus:
Kompexe Fibonacci-Funktion
Wir haben bereits gesehen, dass wir die Fibonaccifolge auf eine komplexwertige Funktion mit reellen Eingabewerten erweitern können. Nun können wir dieses Konzept noch weiter abstrahieren, indem wir auch komplexe Eingabewerte zulassen:
[math] \begin{array}{rl} f:&\mathbb{C}\to\mathbb{C}\\&x\mapsto f(z)=\frac{\Phi^z-(1-\Phi)^z}{\sqrt{5}} \end{array} [/math]
Zugegeben, dies hat nun nicht mehr viel mit der ursprünglichen Fibonacci-Folge als Folge natürlicher Zahlen zu tun. Da die Darstellung komplexer Funktionen immer etwas kompliziert ist, zeigen wir mehrere Darstellungsmöglichkeiten:
Mit Geogebra (Bemerkung: Da Geogebra keine sonderlich exakte Berechnung ermöglicht, sind diese Bilder etwas ungenauer):
Interaktive Darstellung mittels Geogebra:
https://www.geogebra.org/m/qhrggvtr
Nullstellen
Wie man bereits anhand der Bilder (mehr oder weniger gut) erkennen kann, liegen alle Nullstellen auf einer Gerade durch den Nullpunkt. Genauer lassen sich alle Nullstellen [math]z_0[/math] darstellen als:
[math]z_0=n\cdot\frac{2\pi}{\ln(\Phi)-\ln(1-\Phi)}\qquad n\in\mathbb{Z}[/math]
| Beweis |
| .
Es gilt: [math] \begin{array}{rcll} f(z)=\frac{\Phi^z-(1-\Phi)^z}{\sqrt{5}}&=&0&\\ \Phi^z&=&(1-\Phi)^z&\\ z\cdot\ln(\Phi)&=&z\cdot\ln(1-\Phi)+2\pi n&\qquad n\in\mathbb{Z}\\ z&=&n\cdot\frac{2\pi}{\ln(\Phi)-\ln(1-\Phi)}&\qquad n\in\mathbb{Z} \end{array} [/math] |