Fibonacci Folge

Die Fibonacci-Folge ist eine Folge reeller Zahlen.

Erweiterung auf ganze Zahlen

Die Bildungsvorschrift lässt sich einfach umstellen:

[math] f_{n}=f_{n+2}-f_{n+1} [/math]

Damit erhält man eine erweiterte Fibonacci-Folge:

[math] \cdots\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} f_{-7} & f_{-6} & f_{-5} & f_{-4} & f_{-3} & f_{-2} & f_{-1} & f_0 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7\\\hline 13 & -8 & 5 & -3 & 2 & -1 & 1 & 0 & 1 & 1 & 2 & 3 & 5 & 8 & 13 \end{array} \cdots [/math]

Die Beträge der Werte sind symmetrisch, im Negativen alternieren sie jedoch. Dementsprechend nähert sich das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen im Negativen gegen [math]-\frac{1}{\Phi}[/math] an.

Kontinuierliche Fibonacci-Funktion

Formel von Moivre-Binet

Die Formel von Moivre und Binet ist eine Formel zur expliziten Berechung der n-ten Fibonacci-Zahl:

[math] f_n=\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}[/math]

[math]\Phi[/math] ist dabei der goldener Schnitt [math]\Phi=\frac{1+\sqrt{5}}{2}[/math]. Diese Formel liefert für ganzzahlige Werte für n auch exakte, ganzzahlige Ergebnisse.

Beweis durch vollständige Induktion

. Um zu zeigen, dass diese Formel die Fibonacci-Zahlen ergibt, überprüfen wir die Bildungsvorschrift: IA: Die Formel gilt für [math]n=0\ \left(\frac{\Phi^0-(1-\Phi)^0}{\sqrt{5}}=\frac{1-1}{\sqrt{5}}=0=f_0\right)[/math] und für [math] n=1\ \left( f_1= \frac{\Phi^1-(1-\Phi)^1}{\sqrt{5}}=\frac{\sqrt{5}}{\sqrt{5}}=1=f_1\right)[/math]. IV: Nun gelte sie für ein [math] n,\ n-1\in\mathbb{N}[/math]. IS: Dann gilt: [math] \begin{array}{rl} f_{n+1}=f_{n}+f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n+\Phi^{n-1}-(1-\Phi)^{n-1}}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(1+\Phi)-(1-\Phi)^{n-1}\left(1+(1-\Phi)\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(\Phi^2)-(1-\Phi)^{n-1}(1-\Phi)^2}{\sqrt{5}}\\ &=\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\sqrt{5}} \end{array} [/math] Ebenso für negative Zahlen: [math] \begin{array}{rl} f_{n-2}=f_{n}-f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n-\Phi^{n-1}+(1-\Phi)^{n-1}}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(\Phi-1)-(1-\Phi)^{n-1}\left((1-\Phi)-1\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}\left(\frac{1}{\Phi}\right)-(1-\Phi)^{n-1}\left(\frac{1}{1-\Phi}\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-2}-(1-\Phi)^{n-2}}{\sqrt{5}} \end{array} [/math]

Erweiterung auf eine kontinuierliche Funktion

Nun stellt sich die Frage, was passiert, wenn wir in die Formel von Moivre-Binet nicht-ganzzahlige Werte für n einsetzen, die Fibonacci-Folge also in eine kontinuierliche Funktion umwandeln. Da [math]1-\Phi[/math] jedoch negativ ist, und nicht-ganzzahlige Potenzen von negativen Zahlen nur im Komplexen definiert sind, müssen wir den Wertebereich auf [math]\mathbb{C}[/math] erweitern:

[math] \begin{array}{rl} f:&\mathbb{R}\to\mathbb{C}\\&x\mapsto f(x)=\frac{\Phi^x-(1-\Phi)^x}{\sqrt{5}} \end{array} [/math]

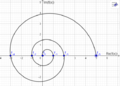
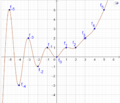
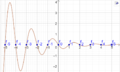
Der Graph dieser Funktion sieht wie folgt aus (Darstellung als Kurve mit Kurvenparameter x):

• 

  [math] -5\leq x\leq0[/math]

• 

  [math] 0\leq x\leq5[/math]

Eine andere Darstellung sieht wie Folgt aus:

• 

  Realteil der Moivre-Binet-Funktion

• 

  Imaginärteil der Moivre-Binet-Funktion

Kompexe Fibonacci-Funktion

Wir haben bereits gesehen, dass wir die Fibonaccifolge auf eine komplexwertige Funktion mit reellen Eingabewerten erweitern können. Nun können wir dieses Konzept noch weiter abstrahieren, indem wir auch komplexe Eingabewerte zulassen. Zugegeben, dies hat nun nicht mehr viel mit der ursprünglichen Fibonacci-Folge als Folge natürlicher Zahlen zu tun. Da die Darstellung komplexer Funktionen immer etwas kompliziert ist, zeigen wir mehrere Darstellungsmöglichkeiten:

• 

  Darstellung mittels Domain colouring