Lemma von Riesz und Folgerungen
Das Lemma von Riesz ist eine bedeutende Aussage eigentlich der Funktionalanalysis. Jedoch kann man mit ein paar grundliegenden Konzepten relativ starke Aussagen über die Beschaffenheit von normierten Vektorräumen sagen. Eine dieser Aussagen wird das Ziel dieses Artikels sein. Das Lemma von Riesz gibt die Grundlage eines Beweises für ein Kriterium über Endlichdimensionalität eines normierten Vektorraumes. Dieses Kriterium wird dementsprechend auch in der Literatur Kompaktheitssatz von Riesz genannt. Um dieses Resultat zu beweisen ist es jedoch notwendig erstmal das Lemma von Riesz einzuführen und zu beweisen.
Motivation
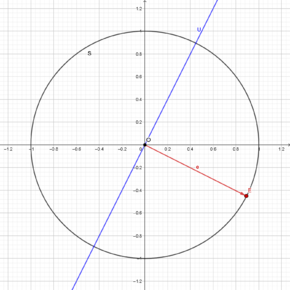
Das Lemma von Riesz wird uns eine Aussage über die Lage von abgeschlossenen echten Unterräumen zur Einheitsphäre [math]\{x\in\mathbb{X}\mid\|x\|=1\}[/math] eines normierten Raums [math]\mathbb{X}[/math] liefern. Genauer beschäftigt sich diese Aussage mit dem möglichst größtem Abstand von Punkten in der Einheitssphäre zu einem gewählten abgeschlossenen echten Unterraum.
Betrachten wir ein paar einfache Fälle und wählen dafür [math]\mathbb{X}=\mathbb{R}^2[/math] mit zugehöriger Einheitsphäre [math]\mathbb{S}^1:=\{x\in\mathbb{R}^2\mid\|x\|=1\}[/math], wobei [math]\|\cdot\|[/math] die euklidische Norm bezeichne. Sei nun [math]U[/math] ein abgeschlossener echter Unterraum in [math]\mathbb{R}^2[/math]. Also ist [math]U[/math] entweder leer oder es handelt sich um einen Ursprungsgerade. Betrachten wir den nicht-trivialen Fall, so haben wir eine Gerade in der Ebene, die den Ursprung schneidet. Ganz anschaulich (Abb. 1) können wir nun einen auf [math]U[/math] senkrecht stehenden normierten Vektor (beim Ursprung) [math]e\in\mathbb{S}^1[/math] wählen und erkennen, dass [math]e[/math] offenbar den maximalen Abstand [math]\big([/math]aller Punkte in [math]\mathbb{S}^1\big)[/math] zu [math]U[/math].
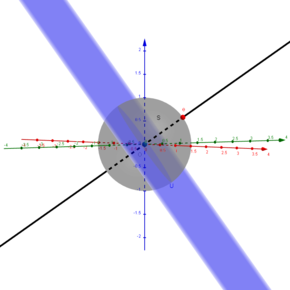
Sei nun [math]\mathbb{X}=\mathbb{R}^3[/math], [math]\mathbb{S}^2:=\left\{x\in\mathbb{R}^3\mid\|x\|=1\right\}[/math] und [math]U[/math] wieder ein abgeschlossener echter (nicht-leerer) Unterraum in [math]\mathbb{R}^3[/math]. Es ist nach kurzer Überlegung klar, dass [math]U[/math] also entweder wieder eine Gerade oder aber eine Fläche ist, die den Ursprungspunkt enthält. Nun ist die gleiche Überlegung wie oben möglich: Wähle einen auf [math]U[/math] senkrecht stehenden normierten Vektor [math]e\in\mathbb{S}^2[/math] (Abb. 2). Ist [math]U[/math] eine Ursprungsgerade, so gibt es unendliche viele Möglichkeiten dieses [math]e[/math] zu wählen. Auch hier hat [math]e[/math] offenbar den maximalen Abstand zu [math]U[/math] auf [math]\mathbb{S}^2[/math].
Der Begriff "senkrecht" ist ein Begriff eines Skalarprodukts, welches im Allgemeinen auf normierten Räumen nicht existieren muss und somit lässt sich unsere Art der Konstruktion von [math]e[/math] nicht beliebig fortsetzen. Trotzdem lässt sich eine verallgemeinerte Aussage treffen.
Das Lemma von Riesz
Das Lemma von Riesz beschreibt eine interessante Eigenschaft in einem normierten Raum [math]\mathbb{X}[/math]. Nämlich: Sei [math]U[/math] ein abgeschlossener Unterraum von [math]\mathbb{X}[/math] und [math]U \neq \mathbb{X}[/math], dann existiert für beliebiges [math]\delta \in (0,1)[/math] ein Vektor [math]x_{\delta} \in \mathbb{X}[/math] mit [math]\Vert x_\delta \Vert =1[/math], sodass [math] \Vert x_\delta - u \Vert \geq \delta [/math] für alle [math]u \in U[/math] gilt. Anschaulich heißt das, dass wir für einen vorgegebenen Abstand [math]\delta\in(0,1)[/math] einen normierten Punkt [math]x\in\mathbb{X}[/math] finden, der zum abgeschlossenen echten Unterraum [math]U[/math] einen Abstand von mindestens [math]\delta[/math] hat. In Quantoren für einen normierten Raum [math]\mathbb{X}[/math] und einem abgeschlossenen echten Unterraum [math]U\subset\mathbb{X}[/math]:
- [math] \begin{equation} \forall\delta\in(0,1)\exists x_\delta\in\mathbb{X}\text{ mit }\|x\|=1:\inf_{u\in U}\|x-u\|\geq\delta \end{equation} [/math]
Beweis
Zunächst sei ohne Einschränkungen [math]U\neq\emptyset[/math], denn für beliebige [math]\delta\in(0,1)[/math] ist [math]\inf_{u\in\emptyset}\|x-u\|=\inf(\emptyset)=\infty\gt \delta[/math] nach Definition des Infimums.
Wir wählen zuerst [math] x \in \mathbb{X}\setminus U [/math]. Dadurch dass [math] U [/math] abgeschlossen ist können wir folgern, dass [math] d:=\inf_{u \in U}\Vert x-u \Vert \gt 0 [/math]. Das folgt aus der Definition der Abgeschlossenheit in einem normierten Raum. Denn gäbe es ein [math] x \in \mathbb{X}\setminus U [/math], sodass [math] d=\inf_{u \in U}\Vert x-u \Vert=0 [/math], so gäbe es auch eine Folge [math](u_n)_{n\in \mathbb{N}} [/math], sodass [math] \Vert u_n - x \Vert \rightarrow 0 [/math], was implizieren würde, dass [math]x[/math] im Abschluss von [math]U[/math], also [math]\bar{U}[/math] läge. Da [math]U[/math] abgeschlossen ist, gilt [math] U=\bar{U}[/math] und somit [math] x \in U [/math], was ein Widerspruch zur Annahme [math] x \in \mathbb{X}\setminus U [/math] ist.
Weiter gilt, da [math] \delta \in (0,1) [/math], dass [math]d \lt \frac{d}{\delta} [/math]. Somit existiert ein [math] u_{\delta} \in U [/math] mit [math] \Vert x-u_{\delta} \Vert \lt \frac{d}{\delta} [/math]. Setzen wir also [math] x_{\delta}:= \frac{x-u_\delta}{\Vert x-u_\delta \Vert} [/math], so gilt [math] \Vert x_{\delta} \Vert =1 [/math], was den ersten Teil des Lemmas zeigt.
Für den zweiten Teil sei [math] u \in U [/math] ein beliebiger Punkt. Aufgrund der Konstruktion von [math]x_\delta[/math] gilt die folgende Identität:
- [math] \begin{align} \Vert x_{\delta}-u \Vert &= \left\Vert \frac{x}{\Vert x- u_{\delta}\Vert} - \frac{u_{\delta}}{\Vert x- u_{\delta}\Vert}- u\right\Vert \\ &=\frac{1}{\Vert x- u_{\delta} \Vert} \left\Vert x - (u_{\delta}+\Vert x- u_{\delta}\Vert u)\right\Vert \end{align} [/math]
Per Konstruktion folgt aber auch, dass [math] u_{\delta}+\Vert x- u_{\delta}\Vert u \in U [/math] und daher [math] \left\Vert x - (u_{\delta}+\Vert x- u_{\delta}\Vert u)\right\Vert \geq d [/math]. Daraus folgt dann aus der obigen Gleichung, dass
- [math] \begin{align} \Vert x_{\delta}-u \Vert =\frac{1}{\Vert x- u_{\delta} \Vert} \left\Vert x - (u_{\delta}+\Vert x- u_{\delta}\Vert u)\right\Vert \geq \frac{d}{\Vert x- u_{\delta} \Vert} \end{align} [/math]
und somit [math] \Vert x_{\delta}-u \Vert \gt \delta [/math] aufgrund der Wahl von [math] u_\delta [/math].
Der Kompaktheitssatz von Riesz
Die allgemeine Version des Satzes lässt sich so formulieren:
Ein normierter Vektorraum [math]\mathbb{X}[/math] ist endlichdimensional, genau dann, wenn die abgeschlossene Einheitskugel [math]\mathbb{D}[/math] ein kompakter topologischer Unterraum ist.
Wir beschränken uns hier jedoch mehr auf den spezifischeren Fall, dass [math]\mathbb{X}[/math] ein [math]\mathbb{R}[/math]-Vektorraum ist. Dadurch lässt sich obiger Satz zu folgender Aussage umformulieren:
Ein [math]\mathbb{R}[/math]-Vektorraum [math]\mathbb{X}[/math] ist endlichdimensional, genau dann, wenn [math]\mathbb{D}:= \{v \in \mathbb{X} \mid \Vert v \Vert \leq 1\}[/math] kompakt ist.
Beweis
Sei zunächst [math]\mathbb{X}[/math] endlich dimensional. Wir können den Satz von Heine-Borel, einen zentralen Satz der Analysis ausnutzen. Denn [math]\mathbb{D}[/math] ist beschränkt und abgeschlossen und ist somit auch kompakt. Nun zeigen wir die Rückrichtung per Kontraposition. Sei also [math]\mathbb{X}[/math] unendlichdimensional.Wir konstruieren induktiv eine Folge [math]\left(x_n\right)_{n\in\mathbb{N}}[/math] in [math]\mathbb{D}[/math], welche keine konvergente Teilfolge besitzt. Damit ist [math]\mathbb{D}[/math] nicht folgenkompakt und somit auch nicht kompakt, da in metrischen Räumen (also auch in [math]\mathbb{R}[/math]-Vektorräumen) Folgenkompaktheit äquivalent zu Kompaktheit ist.
Wähle [math]x_1\in\mathbb{X}[/math] beliebig mit [math]\Vert x_1\Vert=1[/math], also insbesondere [math]x\in\mathbb{D}[/math]. Für [math]n\in\mathbb{N}[/math] sei [math]U_n:=\langle x_1,\ldots,x_n\rangle[/math] der Untervektorraum aufgespannt durch [math]\{x_1,\ldots,x_n\}[/math]. Dieser Raum ist nach Konstruktion endlichdimensional, es handelt sich also um einen echten, abgeschlossenen Untervektorraum von [math]\mathbb{X}[/math] und wir können das Lemma von Riesz benutzen.
Sei [math]\delta:=\frac{1}{2}[/math], nach dem Riesz'schen Lemma existiert ein [math]x\in\mathbb{X}\setminus U_n[/math] mit [math]d:=\inf_{y\in U_n}|x-y|\geq1-\delta=\frac{1}{2}[/math] mit [math]\Vert x\Vert=1[/math], also insbesondere [math]|x-x_i|\geq d\gt \frac{1}{2}[/math] für [math]i=1,\ldots,n[/math] und [math]x\in\mathbb{D}[/math]. Definiere nun das nächste Folgenglied [math]x_{n+1}:=x[/math].
Wir haben also unsere Folge definiert und wir zeigen, dass diese [math]\big([/math]in [math]\mathbb{D}\big)[/math] nicht konvergiert. Seien [math]n,m\in\mathbb{N}[/math] mit [math]n\neq m[/math] und sei ohne Einschränkungen [math]n\lt m[/math], dann ist nach Konstruktion [math]x_m\in\mathbb{X}\setminus U_n[/math] und somit [math]|x_m-x_n|\geq\frac{1}{2}[/math]. Also handelt es sich hier um keine Cauchy-Folge und damit insbesondere um eine nicht konvergente Folge.