Museumswächterproblem: Unterschied zwischen den Versionen

Aus FunFacts Wiki
Zur Navigation springen Zur Suche springen
Zeile 49: Zeile 49:
  
 
=== Definition: Färbung ===
 
=== Definition: Färbung ===
−
Sei E die Menge der Ecken eines Polygons und F die abzählbare Menge der Farben (oder Eigenschaften). Eine Färbung <nowiki><math>f<\math> ordnet jeder Ecke eine Farbe zu, es handelt sich also um eine Abbildung <math>f: E\rightarrow F<\math></nowiki>
+
Sei E die Menge der Ecken eines Polygons und F die abzählbare Menge der Farben (oder Eigenschaften). Eine Färbung <math>f</math> ordnet jeder Ecke eine Farbe zu, es handelt sich also um eine Abbildung <math>f: E\rightarrow F</math>
  
 
Wir nennen eine Färbung eine 3-Färbung, falls:
 
Wir nennen eine Färbung eine 3-Färbung, falls:

Version vom 26. März 2021, 18:39 Uhr

Das Museum ist wegen Corona geschlossen, deswegen werden keine Wächter benötigt:-(

Museum Ritter

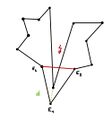
Hier sieht man sehr gut, dass ein Wächter an einer beliebigen Position ausreichend ist.

Zuerst betrachten betrachten wir das Museum Ritter, welches zum gleichnamigen Schokoladenhersteller gehört. Natürlich ist der Grundriss in unserer idealisierten Mathewelt perfekt quadratisch. Der Museumsdirektor möchte nun Museumswächter einstellen und fragt sich, wie viele Leute er anstellen muss, wenn ein Wächter sich zwar nicht frei im Raum bewegen, aber sich um seine Achse drehen darf. Diese Frage ist trivial, es reicht ein Wächter irgendwo im Raum zu positionieren, wie relativ direkt aus der Definition der Konvexität folgt. Wie sieht es aber aus, wenn das Museum einen etwas komplizierteren Grundriss besitzt?

Satz

Nun betrachten wir ein Museum mit einem beliebigen Grundriss, welcher allerdings komplexer ist als der Grundriss des Museum Ritter. Einzige Voraussetzung ist, dass sich alle Wände durch eine Gerade beschreiben lassen. Nun möchte unser Museumsdirektor wieder Wächter einstellen und fragt sich, wie viele er braucht, damit diese das komplette Museum im Blick haben. Auch hier gilt wieder, dass sich die Wächter nicht hin und her bewegen, sondern auf ihren Plätzen bleiben und sich nur um ihre Achse drehen können. Dann benötigt man folgende Anzahl an Wächtern:

Für jedes Museum mit [math]n[/math] Wänden reichen [math]\lfloor \frac{n}{3} \rfloor[/math] Wächter aus.

Beweis nach Steve Fisk

Um diesen Satz zu beweisen, müssen wir zuerst das Museum mathematisch beschreiben können. Dazu führen wir einige Definitionen ein:

Definition: Polygon

Ein Polygon ist ein Tupel [math]P=: \left(P_1,P_2,\dots,P_n \right)[/math], von n verschiedenen Punkten [math]P_i,\ 1\leq i\leq n,\ n\in\mathbb{N}[/math]. Dabei heißen die n Punkte Eckpunkte des Polygons (man spricht auch von einem n-Eck) und die Strecken [math]\overline{P_iP_{i+1}}[/math] für [math] (1\leq i\leq n-1)[/math] und [math]\overline{P_1P_n}[/math] zwischen den Eckpunkten werden als Kanten oder Seiten bezeichnet. Die Verbindungsstrecken zweier Punkte die keinen Kanten sind werden als Diagonalen bezeichnet.
In unserem Fall betrachten wir nur planare Polygone, das heißt n-Ecken, welche in der Ebene liegen. Zusätzlich kann es sein, dass sich die Kanten nicht nur in den Eckpunkten schneiden, in diesem Fall spricht man von einem überschlagenen Polygon.

  • ein überschlagenes Polygon

  • ein konkaves Polygon

  • ein konvexes Polgon

Definition: Triangulation

Als Triangulation eines Polygons bezeichnen wir hier einen planaren Graph, welcher entsteht, wenn man die Innenfläche des Polygons durch Diagonalen, welche sich nicht schneiden, mit Dreiecken ausfüllt.

Für konvexe Polynome ist klar, dass eine Triangulation immer möglich ist

Satz: Für alle ebenen Polygone P existiert eine Triangulation

Beweis: Wir zeigen nun die Aussage für nichtkonvexe Polygone. Sei n die Zahl der Ecken.

IA: für [math]n=3[/math] ist P ein Dreieck also schon trianguliert.

IV: Der Satz gilt für alle Polygone mit weniger als n Ecken

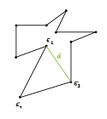
IS: [math]n-1\rightarrow n[/math] Wir suchen eine Diagonale, die P in zwei Polygone [math]P_1[/math] und [math]P_2[/math] teilt. Dazu nehmen wir eine Ecke [math]E_1[/math] mit Innenwinkel kleiner als 180° (existiert immer) und verbinden die beiden zu [math]E_1[/math] benachbarten Ecken [math]E_2[/math] und [math]E_2[/math]. Nun sind 2 Fälle möglich:

Fall 1: [math]\overline{E_2E_3}[/math] ist vollständig in P enthalten. Dann ist mit dieser Diagonal das Polygon in zwei Polygone zerteilt mit jeweils weniger als n Ecken. Nach IV sind diese dann natürlich triangulierbar. Damit folgt die Behauptung auch für das gesamte Polygon.

Fall 2: [math]\overline{E_2E_3}[/math] ist nicht vollständig in P enthalten. Dann liegt also mindestens eine Ecke des Polygons innerhalb des Dreiecks [math]E_1E_2E_3[/math] liegt und kann durch eine Diagonale mit [math]E_1[/math] verbunden werden. Somit lässt sich das Polygon in 2 Polygone mit je weniger als n Ecken teilen, womit nach IV ebenfalls die Behauptung erfüllt ist.

Bemerkung: Im 3-dimensionalen ist eine Triangulation durch Tetraeder jedoch im Allgemeinen nicht möglich (vgl. Schönhardt-Polyeder).

  • Fall 1

  • Fall 2

Definition: Färbung

Sei E die Menge der Ecken eines Polygons und F die abzählbare Menge der Farben (oder Eigenschaften). Eine Färbung [math]f[/math] ordnet jeder Ecke eine Farbe zu, es handelt sich also um eine Abbildung [math]f: E\rightarrow F[/math]

Wir nennen eine Färbung eine 3-Färbung, falls:

(i) [math]\# F=3[/math]

(ii) je 2 benachbarte Ecken stets verschiedene Farben haben

Satz: Jede Triangulation eines Polygons P ist 3-färbbar

Das Polygon hat 17 Ecken, davon vier rote, 7 blaue und 6 gelbe. Wenn man nun einen Wächter in die roten Ecken stellt. so reichen vier Wächter aus. Dies entspricht unserer Erwartung, dass wir höchstens [math] \lfloor \frac{17}{3}\rfloor = 5 [/math] Wächter benötigen.

Beweis: Wir zeigen die Aussage per vollständige Induktion

IA: Für [math]n=3[/math] ist P ein Dreieck und somit die Aussage trivialerweise erfüllt.

IV: Gelte der Satz für Polygone mit weniger als n Ecken

IS: [math]n-1 \rightarrow n[/math] Wir betrachten eine beliebige Triangulierung von [math]P[/math] und wählen zwei beliebige Ecken [math]E_1[/math] und [math]E_2[/math], welche durch eine Diagonale [math]\overline{E_1E_2}[/math] verbunden sind. Da diese das Polygon in zwei Polygone mit weniger als [math]n[/math] Ecken teilt, lässt sich die Induktionsvoraussetzung anwenden, womit die Aussage auch für das zusammengesetze Polygon gilt (seien hierfür o. B. d. A. in beiden Polygonen die Farben von [math]E_1[/math] und [math]E_2[/math] gleich gewählt).

Finaler Beweis nach Fisk:

Für ein Museum mit [math]n=3[/math] Ecken ist die Anzahl der Wächter klar. Für ein Museum mit [math]n\gt 3[/math] Wänden beschreiben wir den Grundriss als Polygon. Wir nutzen nun, dass jedes Polygon triangulierbar und jede Triangulation 3-färbbar ist, wir wählen hierfür o.B.d.A die Farben rot, blau und orange. Mindestens eine dieser Farben muss damit maximal [math]\lfloor \frac{n}{3} \rfloor[/math]-mal vertreten sein, wenn [math]n[/math] die Gesamtzahl der Ecken bezeichnet. In unserer Triangulierung besitzt jedes einzelne Dreieck nach Konstruktion eine rote, eine blaue und eine gelbe Ecke. Besetzt man also alle Ecken einer Farbe mit einer Museumswächter:in, so lässt sich jedes Dreieck (Dreiecke sind konvex) und damit das gesamte Museum einsehen. Somit reichen in jedem Museum [math]\lfloor \frac{n}{3} \rfloor[/math] Wächter aus, um das gesamte Museum zu überblicken.

Beispielrechnung am Guggenheim-Museum Bilbao

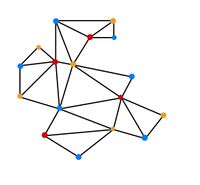
Da er das Museum Ritter so gut mit Wächtern ausgestattet hat, wurde der Direktor befördert und arbeitet nun im renommierten Guggenheim-Museum in Bilbao. Auch hier soll er wieder Wärter anstellen und zwar wieder zu den gleichen Bedingungen wie zuvor. Sie werden also wieder in Ecken positioniert, in denen sie sich drehen, aber nicht ihren Posten verlassen dürfen. Dazu wird, wie in der Nebenstehenden Graphik gezeigt, der Grundriss des Museums trianguliert. Anschließend werden die Ecken wieder gefärbt und gezählt. Dabei ergibt sich eine Anzahl von 27 roten Ecken, 27 orange Ecken und 28 blauen Ecken, also bräuchte man 27 Wächter. Um zu überprüfen, ob sich der Direktor nicht verzählt hat, wendet er noch den Satz des Museumswächterproblems an. Dazu zählt er alle Wände und kommt auf eine Anzahl von insgesamt 85. Nun strengt er seine grauen Zellen an und errechnet damit, dass er höchstens [math] \lfloor \frac{82}{3} \rfloor =27 [/math] Wächter braucht. Dies stimmt mit seinen Erwartungen überein und er ist sehr glücklich.

Trivia

Triangulierung des realen Museum Ritter

Nach ungenauen Berechnungen des Museumsdirektors wird er aus dem Guggenheim-Museum in Bilbao entlassen. So kehrt er ins Museum Ritter zurück. Voller Schreck entdeckt er, dass sich das Museum ja komplett verändert hat. Anstatt eines einfachen Quadrates ist er nun Leiter des realen Museums Ritter, welches im Inneren Wände hat. Zum Glück hat der Direktor in Bilbao genügend Erfahrung im Triangulieren gesammelt, weswegen es nun ein Leichtes für ihn ist, auch das Museum Ritter, mit dem neuen Grundriss, ideal mit Wächterinnen zu besetzen

Ausblick

Nach den langen Reisen unseres lieben Museumdirektors vom Museum Ritter in das Guggenheim-Museum in Bilbao und wieder zurück zum Museum Ritter, überlegt sich der Museumdirektor, was es denn noch für spannende Museen und Aufgaben für Wächterinnen gäben könnte.

So denkt er sich, wieviele Wächterinnen es in einem Museum, welches ein orthogonales Polyeder ist, bräuchte. [math]\lfloor\frac{n}{4}\rfloor[/math] schießt ihm sofort in den Kopf.

Auch hat der Direktor die Überlegung, dass die Wächterinnen die Wände entlang gehen und von jedem Punkt an der Wand in den Raum hineinschauen können. Wieviele Wächterinnen bräuchten er dann?

Und was passiert in Museen, die dreidimensional sind? Wieviele Wächterinnen braucht der Direktor in einem Museum mit Gängen, die quer durch den Raum gehen?

Aber nach all seinen Expeditionen ist er zu müde um auch das zu beweisen.

Quellen

Abgerufen von „https://funfacts.mathi.uni-heidelberg.de/index.php?title=Museumswächterproblem&oldid=1362“