Euklidische Geometrie
Die euklidische Geometrie wurde drei Jahrhunderte v. Chr. von Euklid von Alexandria entwickelt und war über zweitausend Jahre lang die vorherrschende Lehre in diesem Gebiet. Im engsten Sinne bezeichnet sie die von Euklid in seinem Werk Die Elemente dargelegte Geometrie, die sich durch einen klar strukturierten, axiomatischen Aufbau auszeichnet. Als Abgrenzung zu anderen, später entdeckten Geometrien kann man sie aber beispielsweise auch folgendermaßen definieren:
"Geometrien, in denen [zu einer Gerade in einem außerhalb liegenden Punkt] jeweils genau eine Parallele existiert, heißen euklidisch. Geometrien in denen dies nicht der Fall ist, nennt man nicht-euklidisch." [1]
Biographie: Euklid von Alexandria
Leben
Euklid von Alexandria war ein griechischer Mathematiker. Unüblich für Gelehrte der damaligen Epoche, ist wenig über seine Biographie bekannt. Die wenigen vorhandenen Informationen stammen fast ausschließlich aus Berichten anderer Gelehrter seiner Zeit oder sogar erst denen späterer Jahrhunderte. Er lebte und wirkte vermutlich im 3. Jhd. v. Chr. im Museion des antiken Alexandria. Er beschäftigte sich mit allen Bereichen der damaligen Mathematik, vor allem aber mit der Geometrie und der Zahlentheorie, bspw. mit Primzahlen. Dabei baute er seine Geometrie auf der Basis von fünf Axiomen und wenigen anderen Definitionen, Postulaten und Propositionen auf.
Einfluss
Diese Geometrie ist die uns vertrauteste Art, die Welt alltäglich zu sehen. Sie erhielt erst mit der Entwicklung anderer Geometrien im 19. Jahrhundert den Namen Euklidische Geometrie, innerhalb derer bspw. die euklidischen Räume und ihre Variationen existieren. Auch andere mathematische Strukturen, Sätze und Beweise sind nach ihm benannt, wie etwa das Verfahren des Euklidischen Algorithmus zum Ermitteln des größten gemeinsamen Teilers ([math] ggT [/math]) zweier Zahlen, der euklidische Höhen- und Kathetensatz für rechtwinklige Dreiecke und der Satz von Euklid als Beweis dafür, dass es unendlich viele Primzahlen gibt. Weitere von ihm entwickelte Verfahren umfassen u. a. auch eine geometrische Konstruktion der Goldenen Zahl [math]\Phi[/math].[2][3][4]
Schriftwerke
Euklids Werke umfassen nicht nur das, was wir heutzutage unter Mathematik verstehen, sondern auch andere damals im Rahmen der Mathematik behandelte Bereiche wie etwa die Astronomie, Musiktheorie und Optik. Für diese Bereiche stehen die Werke Phainomena, Optika, sowie Die Teilung des Kanon. Seine sieben mathematischen Werke sind Die Elemente, Data, Porisma, Pseudaria, Über die Teilung von Figuren, Oberflächenörter, Kegelschnitte. Nicht alle seiner Bücher sind überliefert, einige gelten als verschollen, andere Werke werde ihm fälschlicherweise zugeschrieben.
Unter den überlieferten Arbeiten befindet sich auch das für diesen Artikel besonders relevante Buch "Elemente" (Stoicheia), eigentlich eine Sammlung von 13 Büchern (diese wurden später von anderen Mathematikern auf 15 erweitert). Die Elemente sind eine umfassende, wenn auch nicht allumfassende Darstellung des mathematischen Wissens der damaligen Zeit. Zusammengetragen werden nicht nur Euklids eigene Arbeit, sondern auch die Erkenntnisse anderer griechischer Mathematiker. Zudem ist das Buch eines der ersten Musterbeispiele für mathematische Strenge bei der deduktiven Beweisführung und wurde über fast zwei Jahrtausende als Standardwerk und Lehrbuch zugleich verwendet. In diesem Rahmen besaß es annähernd den Verbreitungsgrad der Bibel. Seine Leistung besteht aus der strukturierten, bearbeiteten Sammlung des Wissens und ihrer kohärenten Darstellung.[5][6][7]
Definitionen, Axiome, Postulate in den Elementen
Im ersten Buch der Elemente werden 23 Definitionen, 5 Axiome und 5 Postulate aufgeführt, da Euklid die Geometrie als eine deduktive Wissenschaft aufzubauen versuchte. Also gab er zuerst die folgenden unbeweisbaren Grundlagen:
Definitionen
- Punkt ist, was ohne Teil ist.
- Linie ist Länge ohne Breite.
- Die Enden einer Linie sind Punkte.
- Gerade ist eine Linie, die gleichmäßig zu den Punkten auf ihr liegt.
- Fläche ist, was nur Länge und Breite hat.
- Die Enden einer Fläche sind Linien.
- Ebene ist eine Fläche, die gleichmäßig zu den Strecken auf ihr liegt.
- Ebener Winkel ist die Neigung zweier Linien in einer Ebene, die sich treffen und nicht gerade fortsetzen.
- Sind die Linien Geraden, heißt der Winkel geradlinig.
- Bildet eine Gerade, auf eine andere Gerade gestellt, gleiche Nebenwinkel, so sind die beiden gleichen Winkel Rechte. Die Gerade heißt senkrecht zu der, auf die sie steht.
- Stumpf ist ein Winkel, der größer als ein Rechter ist.
- Spitz, wenn kleiner als ein Rechter.
- Grenze ist das, worin etwas endet.
- Figur ist, was von Grenzen umfasst wird.
- Kreis ist eine ebene Figur, von einer Linie umfasst, sodass alle Strecken, die vom einem Punkt im Inneren bis zur Linie laufen, einander gleich sind.
- Mittelpunkt des Kreises heißt der Punkt.
- Durchmesser des Kreises ist jede Strecke, die durch den Mittelpunkt geht und auf beiden Seiten vom Kreisumfang begrenzt ist; eine solche Strecke halbiert den Kreis.
- Halbkreis ist die vom Durchmesser und dem durch ihn abgeschnittenen Bogen umfasste Figur.
- Geradlinig sind von Strecken umfasste Figuren: Dreiseite bei 3 Strecken, Vierseite bei 4 Strecken, Vielseite bei mehr umfassenden Strecken.
- Unter den Dreiseiten hat das gleichseitige Dreieck drei gleiche Seiten, das gleichschenklige Dreieck nur zwei gleiche Seiten, das ungleichseitige Dreieck drei verschiedene Seiten.
- Unter den Dreiseiten gibt es auch das rechtwinklige Dreieck, das einen rechten Winkel hat, das stumpfwinklige Dreieck mit einem stumpfen Winkel und das spitzwinklige Dreieck, das 3 spitze Winkel hat.
- Unter den Vierseiten ist das Quadrat sowohl gleichseitig als rechtwinklig; ein Rechteck ist rechtwinklig, aber nicht gleichseitig; ein Rhombus ist gleichseitig, aber nicht rechtwinklig; ein Rhomboid hat gleiche Gegenseiten und Gegenwinkel, ohne rechtwinklig oder gleichseitig zu sein; die anderen Vierseite heißen Trapeze.
- Parallelen sind Geraden, die in derselben Ebene liegen und sich auch bei Verlängerung nach beiden Seiten ins Unendliche nicht treffen.[8]
Axiome
- Dinge, die zu dem selben gleich sind, sind auch untereinander gleich.
- Wenn man zu gleichen Dingen Gleiches hinzufügt, sind die Ganzen gleich.
- Wenn man von gleichen Dingen Gleiches abzieht, sind die Reste gleich.
- Dinge, die einander decken, sind gleich.
- Das Ganze ist größer als ein Teil davon.[9]
Postulate
- Von einem Punkt zu einem anderen Punkt kann man eine Strecke ziehen.
- Man kann eine Strecke zu einer Geraden verlängern.
- Man kann einen Kreis mit jedem gegebenen Radius und jedem gegebenen Mittelpunkt ziehen.
- Alle rechten Winkel sind einander gleich.
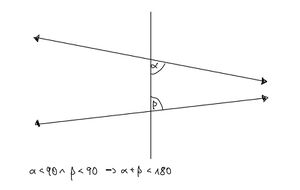
- Wenn bei einer Geraden, die zwei andere Geraden schneidet, die Summe der beiden Innenwinkel (Nachbarwinkel) an der gleichen Seite kleiner ist als die Summe von zwei rechten Winkeln, so werden sich die beiden Geraden auf der Seite schneiden, an der sich diese beiden Winkel befinden.[9]
Das 5. Postulat
Das oben aufgeführte 5. Postulat ist auch unter dem Namen Parallelenaxiom oder auch Parallelenproblem bekannt und wurde jahrhundertelang in der Mathematik diskutiert. Es sticht unter den anderen Axiomen und Postulaten deutlich durch seine Komplexität und Länge hervor. Aus diesem Grund wurde vielfach versucht, es mittels der anderen Annahmen herzuleiten und es somit aus der Liste der Postulate zu streichen und als Präposition einzufügen.[10]
Das Parallelenaxiom wurde später unter anderen durch John Playfair folgendermaßen korrigiert:
- Durch einen gegebenen Punkt außerhalb einer gegebenen Geraden verläuft genau eine Gerade, die parallel zu dieser ist.
Weitere äquivalente Aussagen unter Voraussetzung der übrigen Axiome sind:
- Die Summe der Winkel eines Dreiecks ergibt 180°. (Prop. I.32 Euklid)
- Gegeben sei ein beliebiges Dreieck ABC und eine Strecke DE . Dann gibt es ein Dreieck DEF das ähnlich ist zum Dreieck ABC . (John Wallis)
Die Diskussion um das Parallelenaxiom wurde erst im 19.Jahrhundert insbesondere durch Carl Friedrich Gauß, Lobatschewski und Bolyai beigelegt. Sie konnten zeigen, dass das euklidische Parallenaxiom nicht bewiesen werden kann, indem sie unabhängig voneinander eine neue nicht-euklidische Geometrie entwickelten. Diese verwendet alle Annahmen Euklids mit Ausnahme des 5. Postulats.[10]
Hyperbolische Geometrie
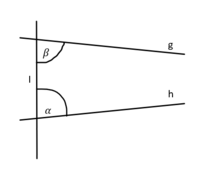
In der hyperbolischen Geometrie wird das Parallelenaxiom durch das sogenannte hyperbolische oder Lobatschewski-Axiom ersetzt:
- Es gibt mehrere zu einer Geraden g parallele Geraden, die durch einen Punkt P verlaufen, welcher nicht auf g liegt.
Auch wenn der Begriff der Parallelität im bisher bekannten Sinn keine Bedeutung hat, lässt sich aus den weiter gültigen Axiomen ableiten, dass zu jeder Geraden g und jedem außerhalb von g liegenden Punkt P unendlich viele Geraden existieren, die mit g in einer Ebene liegen, g aber nicht schneiden.[11]
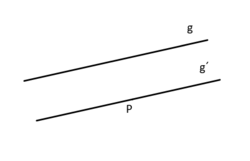
Elliptische Geometrie
- Es gibt keine zu einer Geraden g parallele Geraden, die durch einen Punkt P verlaufen, welcher nicht auf g liegt.
Im ebenen Fall gibt es zu einer gegebenen Geraden g und einem Punkt P, der außerhalb von g liegt, keine Gerade g', die parallel zu g liegt.[1]
Propositionen in den Elementen
Neben den Definitionen, Postulaten und Axiomen enthalten Euklids Elemente, teilweise als erste Quelle, noch eine Vielzahl an mathematischen Resultaten in Form von Propositionen.
Bekannte Beispiele
- Kongruenzsätze im Dreieck (Buch 1, Propositionen 4, 7, 8 und 26)
- Winkelsumme im Dreieck (Buch 1, Proposition 32)
- Satz des Pythagoras (Buch 1, Proposition 47)
- Binomische Formeln (Buch 2, Propositionen 4 und 5)
- Satz des Thales (Buch 3, Proposition 31)
- Konstruktion des regelmäßigen Fünfecks (Buch 4, Proposition 11)
- Erster Strahlensatz (Buch 6, Proposition 2)
- Ähnlichkeitsätze im Dreieck (Buch 6, Proposition 4)
- Teilung einer Strecke im Verhältnis des Goldenen Schnitts (Buch 6, Proposition 30)
- Euklidischen Algorithmus (Buch 7, Proposition 2)
- Existenz unendlich vieler Primzahlen (Satz von Euklid) (Buch 9, Proposition 20)
- Irrationalität der Quadratwurzel von 2 (Buch 10, Proposition 10)
- Klassifikation der platonischen Körper (Buch 13, Proposition 18a)
Kongruenz & Ähnlichkeit
Kongruente Figuren
Zwei Figuren der Ebene heißen kongruent, wenn sie durch eine Kongruenzabbildung (Isometrie) ineinander überführt werden können.
| Kongruenzsatz SSS | Kongruenzsatz SWS | Kongruenzsatz WSW | Kongruenzsatz WWS | Kongurenzsatz WsS |
|---|---|---|---|---|
Ähnliche Figuren
Können sie durch eine Ähnlichkeitsabbildung ineinander überführt werden (Isometrie oder zentrische Streckung), heißen sie ähnlich.[9]
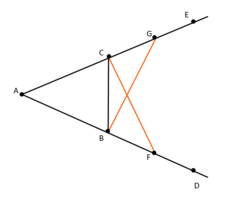
Im Folgenden wird exemplarisch Proposition 1.5 aus Buch 1 bewiesen.
Proposition 1.5
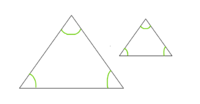
Im gleichschenkligen Dreieck sind die Winkel an der Grundlinie einander gleich, und werden die anderen beiden, gleichen Seiten verlängert, so sind auch die Winkel unterhalb der Grundlinie einander gleich.
Beweis
Sei △ABC ein gleichschenkliges Dreieck mit AB = AC. Dabei sollen die Punkte D und E so liegen, dass [AD] und [AE] die Verlängerungen von [AB] und [AC] sind. (Post.2)
Zu zeigen ist nun: ∠ABC = ∠BCA und ∠CBD = ∠ECB.
Zunächst werden einige vorbereitende Konstruktionen benötigt (in der Skizze rechts schon eingezeichnet):
- Wähle auf [BD] einen Punkt F beliebig. (Def. 4)
- Trage auf [AE] die kürzere Strecke ab, so dass AG = AF gilt. (Prop. 3)
- Konstruiere von C nach F die Strecke [CF] und von B nach G [BG]. (Post. 1)
Schritt 1:
- Da gilt AF = AG, ∠CAB = ∠GAF und AB = AC, folgt mit Kongruenzsatz SWS △ACF ≅ △ABG und dementsprechend CF = BG, ∠FCA = ∠ABG und ∠AGB = ∠AFC. (Prop. 4)
Schritt 2:
- Wegen AF = AG und AB = AC ist auch BF = CG (Ax. 3). Dann gilt mit Schritt 1 ∠BGC = ∠AGB = ∠AFC = ∠BFC.
- Wendet man erneut den Kongruenzsatz SWS an, ergibt sich △BCF ≅ △BCG, d.h. ∠CBF = ∠GCB und ∠FCB = ∠CBG. (Prop.4)
Schritt 3:
- Mit den Ergebnissen der Schritte 1&2 ergibt sich: ∠FCA = ∠ABG = ∠ABC + ∠CBG = ∠ABC + ∠FCB, außerdem gilt ∠FCA = ∠BCA + ∠FCB.
- Setzt man diese Gleichungen gleich, dann ist ∠ABC = ∠BCA. (Ax. 3)
Hiermit ist der erste Teil der Proposition gezeigt.
- Weiter ist mit Schritt 2 ∠CBD = ∠CBF = ∠GCB = ∠ECB.
Dies beweist den zweiten Teil der Proposition. [12]
Moderne Umformulierung durch Hilbert
David Hilbert
David Hilbert (1862-1943) gilt als einer der bedeutendsten Mathematiker der Neuzeit. Er beschäftigte sich hauptsächlich mit der axiomatischen Grundlegung der Geometrie, Problemen der Zahlentheorie sowie Fragen der Relativitätstheorie. Im Jahr 1900 stellte er auf dem Internationalen Mathematikerkongress in Paris seine 23 berühmten Probleme vor, die viel Beachtung erregten, jedoch teilweise bis heute ungelöst sind. Eine Beispiel der Lösung eines Probleme ist der Gödelsche Unvollständigkeitssatz. Dieser zeigt allerdings unter anderem, dass die von Hilbert angestrebte vollständige Axiomatisierung der Mathematik nicht gänzlich erfüllbar ist. [13]
Hilbert’sches Axiomensystem
Euklids Elemente blieben bis Ende des 19. Jahrhunderts das allgemeine Standardwerk der axiomatischen Geometrie. Mit dem Aufkommen der Logik und Mengenlehre entstand jedoch die Notwendigkeit eines Zugangs, welcher strengeren Anforderungen genügt. Erste Vorarbeiten lieferten Pasch und Peano, den großen Durchbruch erzielt jedoch Hilbert. Mit den Grundlagen der Geometrie (1899) entwickelte er einen modernen axiomatischen Zugang für die euklidische Geometrie, welcher beispielgebend für axiomatische Theorien in der Mathematik wurde und die moderne Mathematik stark beeinflusste. [5]
Im Gegensatz zu Euklid verzichtet Hilbert auf die explizite Definition von grundlegenden Begriffen (Punkte, Geraden, ...), stattdessen werden diese und ihrer Beziehungen implizit durch Axiome beschrieben:
"Wir denken drei verschiedene Systeme von Dingen: die Dinge des ersten Systems nennen wir Punkte [...]; die Dinge des zweiten Systems nennen wir Geraden [...]; die Dinge des dritten Systems nennen wir Ebenen [...]; Wir denken die Punkte, Geraden, Ebenen in gewissen gegenseitigen Beziehungen und bezeichnen diese Beziehungen durch Worte wie „liegen“, „zwischen“, „parallel“, „congruent“, „stetig“; die genaue und vollständige Beschreibung dieser Beziehungen erfolgt durch die Axiome der Geometrie." [14]
Diese Axiome der Geometrie gliedern sich in fünf voneinander unabhängige Gruppen:
- I. Axiome der Verknüpfung
- II. Axiome der Anordnung
- III. Axiom der Parallelen (Euklidisches Axiom)
- IV. Axiome der Kongruenz
- V. Axiom der Stetigkeit (Archimedisches Axiom)
Ein konkretes Modell für dieses Axiomsystems liefert das kartesische Koordinatensystem, welches beweist, dass das System widerspruchsfrei ist. Tatsächlich ist jede Ebene, die den Axiomen genügt, isomorph zum kartesischen Modell. Somit legt das Hilbert’sche Axiomensystem die klassische ebene Geometrie bis auf Isomorphie fest. Damit zeigt sich auch, dass die oben beschriebene, ebene axiomatische Geometrie und die ebene analytische Geometrie äquivalente Beschreibungen der ebenen (euklidischen) Geometrie liefern. [5]
Weblinks
- Euklidische Geometrie - Lektion der Vorlesung "Geometrische Aspekte in Analysis und Linearer Algebra".
- Euclid's Elements - Website mit mehr Informationen zu Euklids Elementen inkl. Beweisen.
Einzelnachweise und Quellen
- ↑ https://www.antike-griechische.de/Euklid.pdf
- ↑ Struik, Dirk J. (1967) A Concise History of Mathematics, S. 62
- ↑ http://elearning.fim.uni-linz.ac.at/mathe/erratacps/mathematiker/DE_EUKLID_VON_ALEXANDRIA_GRIECH_EUKLEIDES_48.html
- ↑ https://www.spektrum.de/lexikon/physik/euklid/4557
- ↑ Hochspringen nach: 5,0 5,1 5,2 Hendrik Kasten, Denis Vogel: Grundlagen der ebenen Geometrie. Springer 2018.
- ↑ https://www.spektrum.de/lexikon/mathematik/euklid-von-alexandria/2796
- ↑ https://www.spektrum.de/lexikon/mathematik/amp-ldquor-elemente-des-euklid/4403
- ↑ https://www.math.uni-bielefeld.de/~sek/ez/material/geyer.pdf
- ↑ Hochspringen nach: 9,0 9,1 9,2 9,3 https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/28122/manuscript/b49c19c85a49f7e67bd787a4d260e192.pdf/Euklidische_Geometrie.pdf
- ↑ Hochspringen nach: 10,0 10,1 https://de.wikipedia.org/wiki/Parallelenaxiom#%C3%84quivalente_Formulierungen
- ↑ https://www.spektrum.de/lexikon/mathematik/hyperbolische-geometrie/4090
- ↑ https://www.geometrie-und-logik.de/antike/die-elemente/buch-i/#propositionen_euklid_elemente_buch_i
- ↑ https://de.wikipedia.org/wiki/David_Hilbert
- ↑ David Hilbert: Grundlagen der Geometrie (1. Auflage), veröffentlicht in: Festschrift zur Feier der Enthüllung des Gauß-Weber-Denkmals in Göttingen. Teubner, Leipzig 1899.
Autorinnen
Hannah Maya Pompetzki, Lea Homann, Sophia Künzig, Isabel Giray