Bertrand'sches Sehnen-Paradoxon: Unterschied zwischen den Versionen
K (LeStoe11 verschob die Seite Bertrandsches Sehnen Paradoxon nach Bertrand'sches Sehnen-Paradoxon) |
(Neue Sektion über Jaynes und Bilder) |
||
| Zeile 14: | Zeile 14: | ||
<math> p_1 = \frac{1}{\pi-0} \cdot \left( \frac{2\pi}{3} - \frac{\pi}{3} \right) = \frac{1}{3}. </math> | <math> p_1 = \frac{1}{\pi-0} \cdot \left( \frac{2\pi}{3} - \frac{\pi}{3} \right) = \frac{1}{3}. </math> | ||
| + | [[Datei:Methode 1.png|alternativtext=Darstellung von Methode 1 zur Konstruktion der Verteilung der Sehnen|mini|Darstellung von Methode 1 zur Konstruktion der Verteilung der Sehnen]] | ||
== Methode 2: zufälliger Radius<ref name=":0" /> == | == Methode 2: zufälliger Radius<ref name=":0" /> == | ||
| Zeile 34: | Zeile 35: | ||
<math> p_2 = \frac{1}{1-(-1)} \cdot \left( \frac{1}{2} - \left(-\frac{1}{2}\right) \right) = \frac{1}{2}. | <math> p_2 = \frac{1}{1-(-1)} \cdot \left( \frac{1}{2} - \left(-\frac{1}{2}\right) \right) = \frac{1}{2}. | ||
</math> | </math> | ||
| + | [[Datei:Methode 2.png|alternativtext=Darstellung von Methode 2 zur Konstruktion der Verteilung der Sehnen|mini|Darstellung von Methode 2 zur Konstruktion der Verteilung der Sehnen]] | ||
== Methode 3: zufälliger Sehnen-Mittelpunkt<ref name=":0" /> == | == Methode 3: zufälliger Sehnen-Mittelpunkt<ref name=":0" /> == | ||
| Zeile 49: | Zeile 51: | ||
<math> p_3 = \frac{1}{\pi\cdot1^2} \cdot \left( \pi \cdot \left(\frac{1}{2}\right)^2 - \pi \cdot 0^2 \right) = \frac{1}{4}. | <math> p_3 = \frac{1}{\pi\cdot1^2} \cdot \left( \pi \cdot \left(\frac{1}{2}\right)^2 - \pi \cdot 0^2 \right) = \frac{1}{4}. | ||
</math> | </math> | ||
| + | [[Datei:Methode 3.png|alternativtext=Darstellung von Methode 3 zur Konstruktion der Verteilung der Sehnen|mini|Darstellung von Methode 3 zur Konstruktion der Verteilung der Sehnen]] | ||
==Methode 4: zwei zufällige Punkte<ref>https://www.youtube.com/watch?v=Zqs8_vqf-nI</ref>== | ==Methode 4: zwei zufällige Punkte<ref>https://www.youtube.com/watch?v=Zqs8_vqf-nI</ref>== | ||
| Zeile 67: | Zeile 70: | ||
<math> p_4 = \frac{1}{\pi \cdot 1^2} \cdot \left( \frac{3\sqrt{3}}{4} + \frac{\pi}{3} - \frac{\sqrt{3}}{4} \right) = \frac{1}{3} + \frac{\sqrt{3}}{2\pi} \approx 0.609. | <math> p_4 = \frac{1}{\pi \cdot 1^2} \cdot \left( \frac{3\sqrt{3}}{4} + \frac{\pi}{3} - \frac{\sqrt{3}}{4} \right) = \frac{1}{3} + \frac{\sqrt{3}}{2\pi} \approx 0.609. | ||
</math> | </math> | ||
| + | [[Datei:Methode 4.png|alternativtext=Darstellung von Methode 4 zur Konstruktion der Verteilung der Sehnen|mini|Darstellung von Methode 4 zur Konstruktion der Verteilung der Sehnen]] | ||
=Numerische Vergleiche<ref name=":0" />= | =Numerische Vergleiche<ref name=":0" />= | ||
| Zeile 80: | Zeile 84: | ||
Datei:Center-4.png|Darstellung der Mittelpunkte je 10000 zufälligen Sehnen mit Methode 4. | Datei:Center-4.png|Darstellung der Mittelpunkte je 10000 zufälligen Sehnen mit Methode 4. | ||
</gallery> | </gallery> | ||
| + | |||
| + | =Jaynes Lösung für das Sehnenparadoxon<ref>https://en.wikipedia.org/wiki/Bertrand\_paradox\_(probability)</ref>= | ||
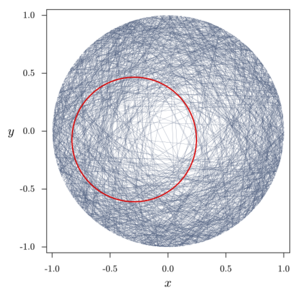
| + | 1973 beschreibt Edwin Jaynes eine Lösung für das Sehnenparadoxon. Er argumentiert, dass eine Lösung nicht von Skalierung und Verschiebung abhängig seien darf,. da diese Aspekte nicht Teil der Problembeschreibung sind. Legen wir also einen beliebigen Kreis in eine der Darstellungen aus [[Bertrand'sches Sehnen-Paradoxon#Numerische Vergleiche|Numerische Vergleiche]] müsste die Verteilung im Kreis der Verteilung im ursprünglichen Kreis entsprechen. | ||
| + | [[Datei:Bertrand3-translate ru.png|alternativtext=Die Verteilung der Sehnen ist nicht invariant unter Skalierung und Verschiebung.|mini|Die Verteilung der Sehnen ist nicht invariant unter Skalierung und Verschiebung.]] | ||
| + | |||
| + | Betrachten wir die Darstellung der Sehnen, so erfüllt nur Methode 2 Jaynes Anforderungen. Jayne schlussfolgert hieraus, dass Methode 2 die Lösung des Sehnenparadoxon ist und Methoden 1, 3 und 4 keine Lösung liefern. | ||
| + | |||
| + | 2015 argumentiert Alon Drory, dass nach Jaynes Anforderungen ebenfalls die anderen Methode korrekt sind. Da Jaynes ursprüngliche Lösung auf der Darstellung der Sehnen als zwei Punkte auf dem Rand aufbaut. Dies ist aber auch die Methode nach der in Methode 2 die Sehnen gewählt werden. Betrachten wir zum Beispiel stattdessen die Mittelpunkte der Sehnen, erfüllt nur Methode 3 Jaynes Anforderungen an eine Lösung. | ||
=Siehe auch= | =Siehe auch= | ||
Version vom 30. August 2021, 06:57 Uhr
Das Bertrand’sches Sehnen-Paradoxon wurde zuerst von Joseph Bertrand in seinem Werk ”Calcul des probabilités” präsentiert. Es behandelt die Frage mit welcher Wahrscheinlichkeit auf einem Kreis eine zufällig gewählte Sehne (Strecke zwischen zwei Punkten auf einem Kreis) länger ist als die Kanten eines einbeschriebenen gleichseitigen Dreiecks im Kreis. Es gibt verschiedene Möglichkeiten die Sehnen zufällig zu verteilen, die zu unterschiedlichen Ergebnissen führen. Das Paradoxon zeigt so anschaulich, dass Wahrscheinlichkeiten nicht eindeutig bestimmt seinen müssen, wenn die Methode zur Erzeugung der Eingabe nicht eindeutig bestimmt ist.
4 Methoden zur Bestimmung der Wahrscheinlichkeit
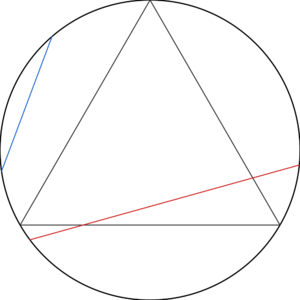
Methode 1: zufällige Endpunkte[1]
Da das Problem rotationssymmetrisch ist, sei o.B.d.A. ein Sehnen-Endpunkt [math] P [/math] fest. Weiterhin stimme ein Eckpunkt des einbeschriebenen gleichseitigen Dreiecks mit [math] P [/math] überein. Ausgehend von der Tangente durch [math] P [/math] an den Kreis betrachte man den im Bogenmaß gemessenen Winkel [math] \Theta [/math] als gleichverteilte Zufallsvariable auf [math] (0, \pi)=(0°, 180°) [/math]. Wegen Symmetrie gilt nun: Die Sehne ist länger als eine Dreiecksseite genau dann, wenn [math] \Theta \in \left(\frac{\pi}{3},\frac{2\pi}{3}\right) = (60°,120°) [/math]. Damit folgt fur die gesuchte Wahrscheinlichkeit:
[math] p_1 = \frac{1}{\pi-0} \cdot \left( \frac{2\pi}{3} - \frac{\pi}{3} \right) = \frac{1}{3}. [/math]
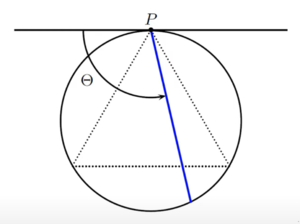
Methode 2: zufälliger Radius[1]
Da das Problem rotationssymmetrisch ist, spielt die Richtung der Sehne keine Rolle, und sei daher o.B.d.A. senkrecht zur [math] X [/math]-Achse in einem Koordinatensystem. Weiterhin liege ein Eckpunkt des einbeschriebenen gleichseitigen Dreiecks auf der [math] X [/math]-Achse. Die zufällige Sehne ist nun eindeutig durch ihren Schnittpunkt [math] U [/math] mit der [math] X [/math]-Achse bestimmt. Da es lediglich auf Längenverhältnisse ankommt, können wir den Einheitskreis betrachten, sodass der Abstand der vertikalen Dreiecksseite zur [math] Y [/math]-Achse genau [math] \frac{1}{2} [/math] beträgt. Nach Identifikation von [math] U [/math] mit dessen [math] X [/math]-Koordinate können wir [math] U [/math] als gleichverteilte Zufallsvariable auf [math] (-1, 1) [/math] annehmen. Es gilt nun:
Die Sehne ist länger als eine Dreiecksseite genau dann, wenn [math] -\frac{1}{2} \lt x \lt \frac{1}{2} [/math].
Damit folgt für die gesuchte Wahrscheinlichkeit:
[math] p_2 = \frac{1}{1-(-1)} \cdot \left( \frac{1}{2} - \left(-\frac{1}{2}\right) \right) = \frac{1}{2}. [/math]
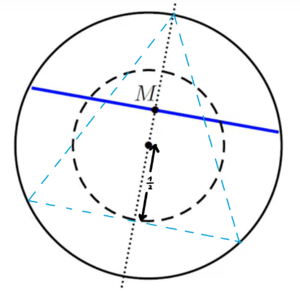
Methode 3: zufälliger Sehnen-Mittelpunkt[1]
Es sei der Sehnen-Mittelpunkt [math] M [/math] gleichverteilt innerhalb der abgeschlossenen Einheitskreisscheibe [math] \{(x,y) \in \mathbb{R}^2 \, | \, x^2 + y^2 \leq 1\} [/math] um den Ursprung. Dann steht die zufällige Sehne senkrecht zur Verbindungsgerade von Kreismittelpunkt und [math] M [/math]. Es gilt nun:
Die Sehne ist länger als eine Dreiecksseite genau dann, wenn [math] M [/math] innerhalb des gestrichelten konzentrischen Kreises mit Radius [math] \frac{1}{2} [/math].
Damit folgt für die gesuchte Wahrscheinlichkeit:
[math] p_3 = \frac{1}{\pi\cdot1^2} \cdot \left( \pi \cdot \left(\frac{1}{2}\right)^2 - \pi \cdot 0^2 \right) = \frac{1}{4}. [/math]
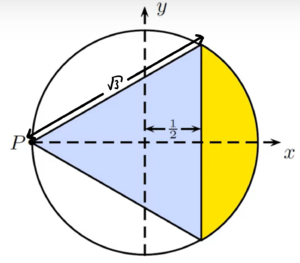
Methode 4: zwei zufällige Punkte[2]
Da das Problem rotationssymmetrisch ist, sei ein Sehnen-Endpunkt [math] P [/math] auf dem Kreisrand fest, sodass dieser auf der [math] X [/math]-Achse eines Koordinatensystems liege. Im einbeschriebenen gleichseitigen Dreieck stimme wieder o.B.d.A. ein Eckpunkt mit [math] P [/math] überein. Der zweite Punkt, durch welchen die Sehne verläuft, sei gleichverteilt innerhalb des Einheitskreises. Dann gilt:
Die Sehne ist länger als eine Dreiecksseite genau dann, wenn der zweite Punkt innerhalb der blauen oder innerhalb der gelben Fläche liegt.
Die blaue Fläche ist mit der Seitenlänge [math] \sqrt{3} [/math] des Dreiecks gleich [math] \frac{3\sqrt{3}}{4} [/math]. Wegen Symmetrie sind die verbleibenden drei Kreissegmente gleich groß und die gelbe Fläche berechnet sich zu [math] \frac{1}{3} \cdot \left( \pi \cdot 1^2 - \frac{3\sqrt{3}}{4} \right) = \frac{\pi}{3} - \frac{\sqrt{3}}{4}. [/math]
Damit folgt für die gesuchte Wahrscheinlichkeit:
[math] p_4 = \frac{1}{\pi \cdot 1^2} \cdot \left( \frac{3\sqrt{3}}{4} + \frac{\pi}{3} - \frac{\sqrt{3}}{4} \right) = \frac{1}{3} + \frac{\sqrt{3}}{2\pi} \approx 0.609. [/math]
Numerische Vergleiche[1]
Die Unterschiede in der Verteilung der Sehnen mit den 4 unterschiedlichen Methoden werden auch bei einer graphischen Darstellung deutlich. An dieser Stelle sind sowohl die Sehnen selbst, als auch die Mittelpunkte der Sehnen dargestellt. Betrachtet man die Verteilung der Sehnen so erscheinen Methode 2 und 4 in dieser Darstellung gleichmäßiger verteilt als Methode 1 und 3, da sich in Methode 1 die Sehnen vermehrt auf den Rand konzentrieren und in Methode 3 deutlich weniger Sehnen durch das Zentrum als durch den äußeren Bereich verlaufen.
Die Darstellung der Mittelpunkte bietet sich an, da Sehnen im Kreis durch ihren Mittelpunkt wohldefiniert sind. In dieser Darstellung erscheint nur Methode 3 gleichmäßig verteilt, bei allen anderen Methode treten die Mittelpunkte vermehrt im Zentrum des Kreises auf. Bei Methode 1 treten zusätzlich noch vermehrt Mittelpunkte am Rand auf.
Jaynes Lösung für das Sehnenparadoxon[3]
1973 beschreibt Edwin Jaynes eine Lösung für das Sehnenparadoxon. Er argumentiert, dass eine Lösung nicht von Skalierung und Verschiebung abhängig seien darf,. da diese Aspekte nicht Teil der Problembeschreibung sind. Legen wir also einen beliebigen Kreis in eine der Darstellungen aus Numerische Vergleiche müsste die Verteilung im Kreis der Verteilung im ursprünglichen Kreis entsprechen.
Betrachten wir die Darstellung der Sehnen, so erfüllt nur Methode 2 Jaynes Anforderungen. Jayne schlussfolgert hieraus, dass Methode 2 die Lösung des Sehnenparadoxon ist und Methoden 1, 3 und 4 keine Lösung liefern.
2015 argumentiert Alon Drory, dass nach Jaynes Anforderungen ebenfalls die anderen Methode korrekt sind. Da Jaynes ursprüngliche Lösung auf der Darstellung der Sehnen als zwei Punkte auf dem Rand aufbaut. Dies ist aber auch die Methode nach der in Methode 2 die Sehnen gewählt werden. Betrachten wir zum Beispiel stattdessen die Mittelpunkte der Sehnen, erfüllt nur Methode 3 Jaynes Anforderungen an eine Lösung.
Siehe auch
Einzelnachweise
Autoren
- Adrian Becker
- Lennart Stöpler
- Timo Dörzbach