Bertrand'sches Sehnen-Paradoxon

Beispiel fur einen Kreis mit einbeschriebenem gleichseitigen Dreieck. Die rote Sehne ist länger als die Dreiecksseiten, die Blaue ist kurzer.

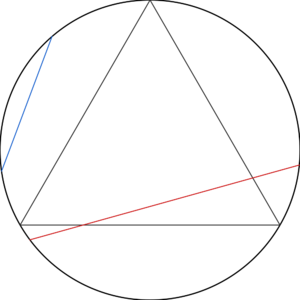
Das Bertrand’sches Sehnen-Paradoxon wurde zuerst von Joseph Bertrand in seinem Werk ”Calcul des probabilités” präsentiert. Es behandelt die Frage mit welcher Wahrscheinlichkeit auf einem Kreis eine zufällig gewählte Sehne (Strecke zwischen zwei Punkten auf einem Kreis) länger ist als die Kanten eines einbeschriebenen gleichseitigen Dreiecks im Kreis. Es gibt verschiedene Möglichkeiten die Sehnen zufällig zu verteilen, die zu unterschiedlichen Ergebnissen führen. Das Paradoxon zeigt so anschaulich, dass Wahrscheinlichkeiten nicht eindeutig bestimmt seinen müssen, wenn die Methode zur Erzeugung der Eingabe nicht eindeutig bestimmt ist.

4 Methoden zur Bestimmung der Wahrscheinlichkeit

Methode 1: zufällige Endpunkte

Da das Problem rotationssymmetrisch ist, sei o.B.d.A. ein Sehnen-Endpunkt [math] P [/math] fest. Weiterhin stimme ein Eckpunkt des einbeschriebenen gleichseitigen Dreiecks mit [math] P [/math] überein. Ausgehend von der Tangente durch [math] P [/math] an den Kreis betrachte man den im Bogenmaß gemessenen Winkel [math] \Theta [/math] als gleichverteilte Zufallsvariable auf [math] (0, \pi)=(0°, 180°) [/math]. Wegen Symmetrie gilt nun: Die Sehne ist länger als eine Dreiecksseite genau dann, wenn [math] \Theta \in \left(\frac{\pi}{3},\frac{2\pi}{3}\right) = (60°,120°) [/math]. Damit folgt fur die gesuchte Wahrscheinlichkeit:

[math] p_1 = \frac{1}{\pi-0} \cdot \left( \frac{2\pi}{3} - \frac{\pi}{3} \right) = \frac{1}{3}. [/math]

Numerische Vergleiche

Die Unterschiede in der Verteilung der Sehnen mit den 4 unterschiedlichen Methoden werden auch bei einer graphischen Darstellung deutlich. An dieser Stelle sind sowohl die Sehnen selbst, als auch die Mittelpunkte der Sehnen dargestellt. Betrachtet man die Verteilung der Sehnen so erscheinen Methode 2 und 4 in dieser Darstellung gleichmäßiger verteilt als Methode 1 und 3, da sich in Methode 1 die Sehnen vermehrt auf den Rand konzentrieren und in Methode 3 deutlich weniger Sehnen durch das Zentrum als durch den äußeren Bereich verlaufen. Die Darstellung der Mittelpunkte bietet sich an, da Sehnen im Kreis durch ihren Mittelpunkt wohldefiniert sind. In dieser Darstellung erscheint nur Methode 3 gleichmäßig verteilt, bei allen anderen Methode treten die Mittelpunkte vermehrt im Zentrum des Kreises auf. Bei Methode 1 treten zusätzlich noch vermehrt Mittelpunkte am Rand auf.

• 

  Darstellung von je 1000 zufälligen Sehnen mit Methode 1.

• 

  Darstellung von je 1000 zufälligen Sehnen mit Methode 2.

• 

  Darstellung von je 1000 zufälligen Sehnen mit Methode 3.

• 

  Darstellung von je 1000 zufälligen Sehnen mit Methode 4.

• 

  Darstellung der Mittelpunkte je 10000 zufälligen Sehnen mit Methode 1.

• 

  Darstellung der Mittelpunkte je 10000 zufälligen Sehnen mit Methode 2.

• 

  Darstellung der Mittelpunkte je 10000 zufälligen Sehnen mit Methode 3.

• 

  Darstellung der Mittelpunkte je 10000 zufälligen Sehnen mit Methode 4.

Autoren

• Adrian Becker
• Lennart Stöpler
• Timo Dörzbach