Hauptseite: Unterschied zwischen den Versionen

Aus FunFacts Wiki
Zur Navigation springen Zur Suche springen
 
(5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
 
<strong>Willkommen!</strong>
 
<strong>Willkommen!</strong>
  
−
Dieses Wiki basiert auf einem Projekt der Vorlesung [https://www.mathi.uni-heidelberg.de/~aschilling/teaching/funfacts-WS20 Fun Facts aus der Analysis und linearen Algebra] an der Uni Heidelberg im Wintersemester 2020/21.
+
Dieses Wiki basiert auf einem Projekt der Vorlesungen [https://www.mathi.uni-heidelberg.de/~aschilling/teaching/funfacts-WS20 Fun Facts aus der Analysis und linearen Algebra] (Wintersemester 2020/21) und [https://www.mathi.uni-heidelberg.de/~aschilling/teaching/geometric_aspects_Sose21 Geometrische Aspekte aus Analysis und linearer Algebra] (Sommersemester 2021) an der Uni Heidelberg.
  
−
== Ganz ganz viele Nummern ==
+
== Ganz ganz viele... ==
 
<gallery>
 
<gallery>
 
Hilberts Hotel Logo.jpg|[[Hilberts Hotel]]
 
Hilberts Hotel Logo.jpg|[[Hilberts Hotel]]
Zeile 19: Zeile 20:
 
Der kleine Satz von Fermat.png|[[Der kleine Satz von Fermat]]
 
Der kleine Satz von Fermat.png|[[Der kleine Satz von Fermat]]
 
Zeta.png|[[Riemannsche Vermutung]]
 
Zeta.png|[[Riemannsche Vermutung]]
 +
</gallery>
 +
 +
== Noch mehr besondere Zahlen ==
 +
 +
<gallery>
 +
Graphische Darstellung.png|[[Pi und das Buffon'sche Nadelproblem]]
 +
Basler Problem.png|[[Basler Problem]]
 +
Goldene Spirale.png|[[Goldener Schnitt]]
 +
Fibonacci Folge.png|[[Fibonacci Folge]]
 +
Zahlbereich.png|[[Konstruktion der reellen Zahlen]]
 
</gallery>
 
</gallery>
  
Zeile 28: Zeile 39:
 
Doubling of a sphere, as per the Banach-Tarski Theorem.png|[[Banach-Tarski-Paradox]]
 
Doubling of a sphere, as per the Banach-Tarski Theorem.png|[[Banach-Tarski-Paradox]]
 
FY1GU.png|[[Arctic Circle Theorem]]
 
FY1GU.png|[[Arctic Circle Theorem]]
 +
Titelbild Magische Quadrate.jpg|[[Magische Quadrate]]
 
</gallery>
 
</gallery>
  
 +
== Bunt, chaotisch und fraktal ==
 +
 +
<gallery>
 +
Julia1.png|[[Mandelbrotmenge]]
 +
LogisticMap BifurcationDiagram.png|[[Die Feigenbaum Konstante]]
 +
Image-11_low.jpg|[[Zufallsmatrizen - Bohemians und die geheimnisvolle Ordnung im Chaos]]
 +
</gallery>
 +
 +
== Spannende Anwendungen ==
 +
 +
<gallery>
 +
Beispiel einer Vierfärbung.png|[[4-Farben-Satz]]
 +
Fall2.jpg|[[Museumswächterproblem]]
 +
Internet 2 (1).jpg|[[PageRank-Algorithmus]]
 +
Blauer Knoten.jpg|[[Anwendungen der Knotentheorie]]
 +
Titel Smith Normalform.png|[[Homologie mit Smith Normalform]]
 +
Annäherungen durch Partialsummen von FS(g).png|[[Fourieranalyse]]
 +
</gallery>
 +
 +
== Unerwartetes ==
 +
 +
<gallery>
 +
Riesz Abbildung02.png|[[Lemma von Riesz und Folgerungen]]
 +
Eine Weierstraß-Funktion.png|[[Gegenbeispiele der Funktionentheorie und Analysis]]
 +
Example.png|[[Bertrand'sches Sehnen-Paradoxon]]
 +
Wahr und Falsch.jpg|[[Gödelsche Unvollständigkeitssätze]]
 +
</gallery>
 +
 +
 +
== Geometrie und Physik ==
 +
 +
<gallery>
 +
Titel Normen und Metriken.png|[[Normen und Metriken]]
 +
Euklids Elemente Papyrus.jpg|[[Euklidische Geometrie]]
 +
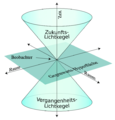
Titel Minkowski Raum.png|[[Hyperbolische Geometrie und Physik - Der Minkowski-Raum]]
 +
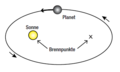
Keplergesetz-1.png|[[Die Keplerschen Gesetze]]
 +
Reskalierter Vektor.jpg|[[Matrixgruppen in der Physik]]
 +
</gallery>
  
−
Hier gibt es eine [https://funfacts.mathi.uni-heidelberg.de/index.php/Anleitung Anleitung] zur Bearbeitung des Wikis.
+
<!--Hier gibt es eine [https://funfacts.mathi.uni-heidelberg.de/index.php/Anleitung Anleitung] zur Bearbeitung des Wikis. -->

Aktuelle Version vom 22. Oktober 2021, 09:31 Uhr

Willkommen!

Dieses Wiki basiert auf einem Projekt der Vorlesungen Fun Facts aus der Analysis und linearen Algebra (Wintersemester 2020/21) und Geometrische Aspekte aus Analysis und linearer Algebra (Sommersemester 2021) an der Uni Heidelberg.

Ganz ganz viele...

Primzahlen

Noch mehr besondere Zahlen

Zauberei?

Bunt, chaotisch und fraktal

Spannende Anwendungen

Unerwartetes


Geometrie und Physik


Abgerufen von „https://funfacts.mathi.uni-heidelberg.de/index.php?title=Hauptseite&oldid=5836“